Question

【题目】已知等比数列{an}满足：|a2﹣a3|=10，a1a2a3=125．
（1）求数列{an}的通项公式；
（2）是否存在正整数m，使得 ？若存在，求m的最小值；若不存在，说明理由．

Answer 1

【答案】
（1）解：设等比数列{an}的公比为q，则由已知可得

解得

故 ．

（2）解：若 ，则 ，

故 是首项为 ，公比为 的等比数列，

从而 ．

若 ，则 是首项为 ，公比为﹣1的等比数列，

从而 故 ．

综上，对任何正整数m，总有 ．

故不存在正整数m，使得 成立．

【解析】（1）设等比数列{an}的公比为q，结合等比数列的通项公式表示已知条件，解方程可求a1 ， q，进而可求通项公式（2）结合（I）可知 是等比数列，结合等比数列的求和公式可求 ，即可判断
【考点精析】关于本题考查的等比数列的通项公式（及其变式）和数列的前n项和，需要了解通项公式：；数列{an}的前n项和sn与通项an的关系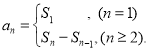才能得出正确答案．