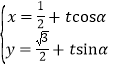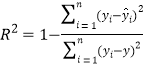题目内容
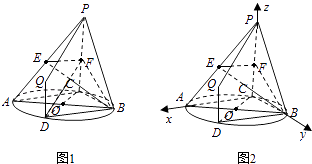
【题目】如图,AB是圆O的直径,点C是圆O上异于A,B的点,直线PC⊥平面ABC,E,F分别是PA,PC的中点. 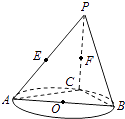
(1)记平面BEF与平面ABC的交线为l,试判断直线l与平面PAC的位置关系,并加以证明;
(2)设(1)中的直线l与圆O的另一个交点为D,且点Q满足 ![]() .记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.
.记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.
【答案】
(1)解:直线l∥平面PAC,证明如下:
连接EF,因为E,F分别是PA,PC的中点,所以EF∥AC,
又EF平面ABC,且AC平面ABC,所以EF∥平面ABC.
而EF平面BEF,且平面BEF∩平面ABC=l,所以EF∥l.
因为l平面PAC,EF平面PAC,所以直线l∥平面PAC.
(2)解:(综合法)如图1,连接BD,由(1)可知交线l即为直线BD,且l∥AC.
因为AB是⊙O的直径,所以AC⊥BC,于是l⊥BC.
已知PC⊥平面ABC,而l平面ABC,所以PC⊥l.
而PC∩BC=C,所以l⊥平面PBC.
连接BE,BF,因为BF平面PBC,所以l⊥BF.
故∠CBF就是二面角E﹣l﹣C的平面角,即∠CBF=β.
由 ![]() ,作DQ∥CP,且
,作DQ∥CP,且 ![]() .
.
连接PQ,DF,因为F是CP的中点,CP=2PF,所以DQ=PF,
从而四边形DQPF是平行四边形,PQ∥FD.
连接CD,因为PC⊥平面ABC,所以CD是FD在平面ABC内的射影,
故∠CDF就是直线PQ与平面ABC所成的角,即∠CDF=θ.
又BD⊥平面PBC,有BD⊥BF,知∠BDF=α,
于是在Rt△DCF,Rt△FBD,Rt△BCF中,分别可得 ![]() ,
,
从而 ![]() .
.
(向量法)如图2,由 ![]() ,作DQ∥CP,且
,作DQ∥CP,且 ![]() .
.
连接PQ,EF,BE,BF,BD,由(Ⅰ)可知交线l即为直线BD.
以点C为原点,向量 ![]() 所在直线分别为x,y,z轴,建立如图所示的空间直角坐标系,设CA=a,CB=b,CP=2c,则有
所在直线分别为x,y,z轴,建立如图所示的空间直角坐标系,设CA=a,CB=b,CP=2c,则有 ![]() .
.
于是 ![]() ,
,
∴  =
= ![]() ,从而
,从而 ![]() ,
,
又取平面ABC的一个法向量为 ![]() ,可得
,可得 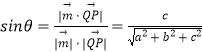 ,
,
设平面BEF的一个法向量为 ![]() ,
,
所以由  可得
可得  取
取 ![]() =(0,c,b),
=(0,c,b),
于是  ,从而
,从而 ![]() .
.
故 ![]() ,即sinθ=sinαsinβ.
,即sinθ=sinαsinβ.
【解析】(1)直线l∥平面PAC.连接EF,利用三角形的中位线定理可得,EF∥AC;利用线面平行的判定定理即可得到EF∥平面ABC.由线面平行的性质定理可得EF∥l.再利用线面平行的判定理即可证明直线l∥平面PAC.(2)综合法:利用线面垂直的判定定理可证明l⊥平面PBC.连接BE,BF,因为BF平面PBC,所以l⊥BC.故∠CBF就是二面角E﹣l﹣C的平面角,即∠CBF=β.已知PC⊥平面ABC,可知CD是FD在平面ABC内的射影,故∠CDF就是直线PQ与平面ABC所成的角,即∠CDF=θ.由BD⊥平面PBC,有BD⊥BF,知∠BDF=α,分别利用三个直角三角形的边角关系即可证明结论;
向量法:以点C为原点,向量 ![]() 所在直线分别为x,y,z轴,建立如图所示的空间直角坐标系,利用两个平面的法向量的夹角即可得出二面角.
所在直线分别为x,y,z轴,建立如图所示的空间直角坐标系,利用两个平面的法向量的夹角即可得出二面角.
【考点精析】解答此题的关键在于理解空间中直线与平面之间的位置关系的相关知识,掌握直线在平面内—有无数个公共点;直线与平面相交—有且只有一个公共点;直线在平面平行—没有公共点,以及对直线与平面平行的判定的理解,了解平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案【题目】在某次测试中,卷面满分为100分,考生得分为整数,规定60分及以上为及格.某调研课题小组为了调查午休对考生复习效果的影响,对午休和不午休的考生进行了测试成绩的统计,数据如下表:

(1)根据上述表格完成下列列联表:
(2)判断“能否在犯错误的概率不超过0.010的前提下认为成绩及格与午休有关”?
(参考公式:![]() ,其中
,其中![]() .)
.)
| 0.010 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |