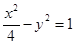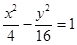题目内容
(2014·武汉模拟)已知点P是圆M:x2+(y+m)2=8(m>0,m≠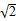 )上一动点,点N(0,m)是圆M所在平面内一定点,线段NP的垂直平分线l与直线MP相交于点Q.
)上一动点,点N(0,m)是圆M所在平面内一定点,线段NP的垂直平分线l与直线MP相交于点Q.
(1)当P在圆M上运动时,记动点Q的轨迹为曲线Г,判断曲线Г为何种曲线,并求出它的标准方程.
(2)过原点斜率为k的直线交曲线Г于A,B两点,其中A在第一象限,且它在x轴上的射影为点C,直线BC交曲线Г于另一点D,记直线AD的斜率为k′,是否存在m,使得对任意的k>0,都有|k·k′|=1?若存在,求m的值;若不存在,请说明理由.
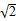 )上一动点,点N(0,m)是圆M所在平面内一定点,线段NP的垂直平分线l与直线MP相交于点Q.
)上一动点,点N(0,m)是圆M所在平面内一定点,线段NP的垂直平分线l与直线MP相交于点Q.(1)当P在圆M上运动时,记动点Q的轨迹为曲线Г,判断曲线Г为何种曲线,并求出它的标准方程.
(2)过原点斜率为k的直线交曲线Г于A,B两点,其中A在第一象限,且它在x轴上的射影为点C,直线BC交曲线Г于另一点D,记直线AD的斜率为k′,是否存在m,使得对任意的k>0,都有|k·k′|=1?若存在,求m的值;若不存在,请说明理由.
(1)双曲线  -
- =1
=1
(2)存在,m=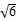
 -
- =1
=1(2)存在,m=
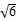
(1)因为|QN|=|QP|,
所以||QM|-|QN||=|PM|=2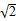 .
.
①当2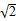 <2m时,动点Q的轨迹曲线Г为以点M,N为焦点,2a=2
<2m时,动点Q的轨迹曲线Г为以点M,N为焦点,2a=2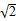 为实轴的双曲线,其标准方程为
为实轴的双曲线,其标准方程为 -
- =1.
=1.
②当2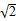 >2m时,动点Q无轨迹.
>2m时,动点Q无轨迹.
(2)如图所示,
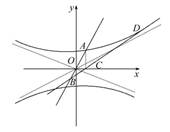
设A(x1,y1),D(x0,y0),则B(-x1,-y1),C(x1,0).
则y1=kx1.
直线BC的方程为y= (x-x1),即y=
(x-x1),即y= (x-x1).
(x-x1).
联立 化为(m2k2-2k2-8)x2-2k2(m2-2)x1x+(m2-2)(k2
化为(m2k2-2k2-8)x2-2k2(m2-2)x1x+(m2-2)(k2 -8)=0.
-8)=0.
所以-x1+x0= ,
,
所以k′= =
=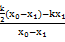
= -
-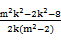 .
.
若存在m,使得对任意的k>0,都有|k·k′|=1,
则 =1,
=1,
整理得m2=6,解得m=±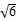 (负值舍去).
(负值舍去).
因此存在m,且当m=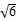 时,满足题意.
时,满足题意.
所以||QM|-|QN||=|PM|=2
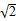 .
.①当2
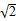 <2m时,动点Q的轨迹曲线Г为以点M,N为焦点,2a=2
<2m时,动点Q的轨迹曲线Г为以点M,N为焦点,2a=2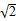 为实轴的双曲线,其标准方程为
为实轴的双曲线,其标准方程为 -
- =1.
=1.②当2
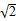 >2m时,动点Q无轨迹.
>2m时,动点Q无轨迹.(2)如图所示,

设A(x1,y1),D(x0,y0),则B(-x1,-y1),C(x1,0).
则y1=kx1.
直线BC的方程为y=
 (x-x1),即y=
(x-x1),即y= (x-x1).
(x-x1).联立
 化为(m2k2-2k2-8)x2-2k2(m2-2)x1x+(m2-2)(k2
化为(m2k2-2k2-8)x2-2k2(m2-2)x1x+(m2-2)(k2 -8)=0.
-8)=0.所以-x1+x0=
 ,
,所以k′=
 =
=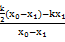
=
 -
-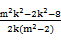 .
.若存在m,使得对任意的k>0,都有|k·k′|=1,
则
 =1,
=1,整理得m2=6,解得m=±
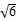 (负值舍去).
(负值舍去).因此存在m,且当m=
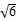 时,满足题意.
时,满足题意.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

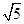 ,0),点P位于该双曲线上,线段PF1的中点坐标为(0,2),则双曲线的方程是( )
,0),点P位于该双曲线上,线段PF1的中点坐标为(0,2),则双曲线的方程是( )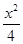 -y2=1
-y2=1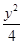 =1
=1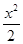 -
-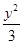 =1
=1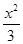 -
-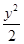 =1
=1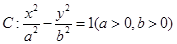 的两个焦点为
的两个焦点为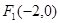 、
、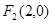 点
点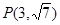 在双曲线C上.
在双曲线C上.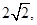 求直线l的方程.
求直线l的方程.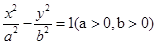 的左、右焦点分别是
的左、右焦点分别是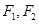 ,过
,过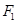 作倾斜角为
作倾斜角为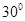 的直线交双曲线右支于点M,若
的直线交双曲线右支于点M,若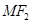 垂直于x轴,则双曲线的离心率为( )
垂直于x轴,则双曲线的离心率为( )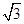
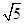
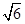
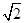
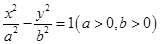 的左、右焦点分别为
的左、右焦点分别为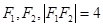 ,P是双曲线右支上的一点,
,P是双曲线右支上的一点,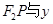 轴交于点A,
轴交于点A,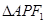 的内切圆在
的内切圆在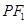 上的切点为Q,若
上的切点为Q,若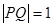 ,则双曲线的离心率是
,则双曲线的离心率是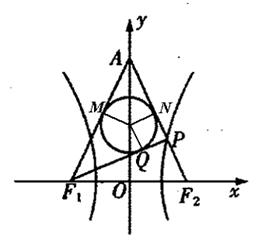
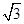
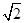
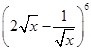 的展开式中含
的展开式中含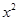 项的系数是
项的系数是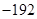 ;
;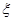 服从正态分布N(2,
服从正态分布N(2,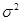 )(
)(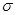 >0).若
>0).若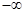 ,1)内取值的概率为0.15,则
,1)内取值的概率为0.15,则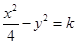 的渐近线方程为
的渐近线方程为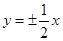 ,则k=1.其中正确命题的序号是 .
,则k=1.其中正确命题的序号是 .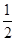 B.
B.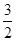 C.
C.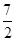 D.5
D.5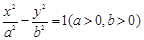 ,
,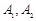 为实轴顶点,
为实轴顶点,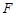 是右焦点,
是右焦点,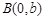 是虚轴端点,
是虚轴端点,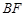 上(不含端点)存在不同的两点
上(不含端点)存在不同的两点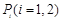 ,使得
,使得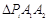 构成以
构成以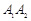 为斜边的
为斜边的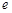 的取值范围是( )
的取值范围是( )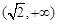
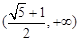
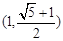
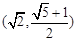
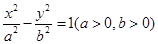 的两个焦点为
的两个焦点为 、
、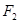 ,其中一条渐近线方程为
,其中一条渐近线方程为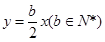 ,
,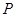 为双曲线上一点,且满足
为双曲线上一点,且满足 (其中
(其中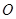 为坐标原点),若
为坐标原点),若 、
、 、
、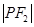 成等比数列,则双曲线
成等比数列,则双曲线 的方程为( )
的方程为( )