题目内容
两圆相交于两点(1,3)和(m,1),两圆的圆心都在直线x-y+
=0上,则m+c=( )
| c |
| 2 |
| A.-1 | B.2 | C.3 | D.0 |
已知两圆相交于两点(1,3)和(m,1),且两圆的圆心都在直线x-y+
=0上,
公共弦的斜率为:-1,经过(1,3)点的公共弦为:y-3=-1(x-1),所以x+y-4=0,
又因为(m,1)在公共弦上,所以m+1-4=0,
解得m=3;
两点(1,3)和(3,1)的中点在连心线x-y+
=0上,
即(2,2)在连心线x-y+
=0上,所以c=0,
所以m+c=3;
故选C.
| c |
| 2 |
公共弦的斜率为:-1,经过(1,3)点的公共弦为:y-3=-1(x-1),所以x+y-4=0,
又因为(m,1)在公共弦上,所以m+1-4=0,
解得m=3;
两点(1,3)和(3,1)的中点在连心线x-y+
| c |
| 2 |
即(2,2)在连心线x-y+
| c |
| 2 |
所以m+c=3;
故选C.

练习册系列答案
相关题目
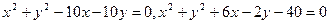 ,求(1)它们的公共弦所在直线的方程;(2)公共弦长。
,求(1)它们的公共弦所在直线的方程;(2)公共弦长。 与
与 的位置关系是( )
的位置关系是( )