题目内容
已知等差数列{an}中,首项a1=1,公差d为整数,且满足a1+3<a3,a2+5>a4,数列{bn}满足bn=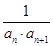 ,其前n项和为Sn.
,其前n项和为Sn.
(1)求数列{an}的通项公式;
(2)若S2为S1,Sm (m∈N*)的等比中项,求正整数m的值.
(3)对任意正整数k,将等差数列{an}中落入区间(2k,22k)内项的个数记为ck,求数列{cn}的前n项和Tn
(1)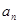 =1+(n1)
=1+(n1)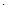 2=2n1;(2)
2=2n1;(2) =12;(3)
=12;(3) .
.
解析试题分析:(1)根据题意先确定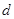 的值,再根据等差数列的通项公式求解;(2)根据(1)所得的通项公式求出
的值,再根据等差数列的通项公式求解;(2)根据(1)所得的通项公式求出 ,利用裂项求和法求出其前
,利用裂项求和法求出其前 项和,再根据等比中项的定义列式求解;(3))对任意正整数k,
项和,再根据等比中项的定义列式求解;(3))对任意正整数k,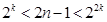 ,则
,则 ,而
,而 ,由题意可知
,由题意可知  ,利用分组求和法可解答.
,利用分组求和法可解答.
试题解析:(1)由题意,得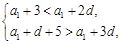 解得
解得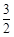 < d <
< d < . 2分
. 2分
又d∈Z,∴d=2.
∴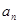 =1+(n1)
=1+(n1)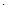 2=2n1. 4分
2=2n1. 4分
(2)∵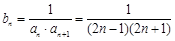
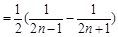 ..6分
..6分
∴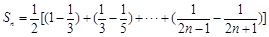
 7分
7分
∵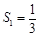 ,
, ,
, ,
, 为
为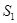 ,
, (
(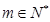 )的等比中项,
)的等比中项,
∴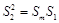 ,即
,即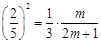 ,
,
解得 =12. .9分
=12. .9分
(3)对任意正整数k,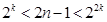 ,则
,则 ,
,
而 ,由题意可知
,由题意可知  , 12分
, 12分
于是 
 ,
,
即 . 14分
. 14分
考点:等差数列的通项公式、裂项求和法、分组求和、等比数列前 项和公式.
项和公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
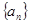 中,
中,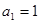 ,公差
,公差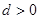 ,且它的第2项,第5项,第14项分别是等比数列
,且它的第2项,第5项,第14项分别是等比数列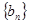 的第2项,第3项,第4项.
的第2项,第3项,第4项.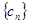 对任意自然数均有
对任意自然数均有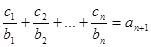 成立,求
成立,求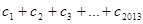 的值.
的值. 的各项都是正数,且对任意
的各项都是正数,且对任意 ,都有
,都有 ,其中
,其中 为数列
为数列 项和。
项和。 的前
的前 的前
的前 项和为
项和为 .且
.且 .
. ,数列
,数列 满足:
满足:

 ,求数列
,求数列 的前
的前 项和
项和 .
.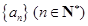 的前
的前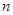 项和为
项和为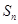 ,且
,且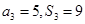 .
.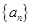 的通项公式;
的通项公式;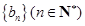 ,若
,若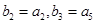 ,求数列
,求数列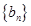 的前
的前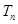
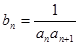 ,求数列
,求数列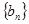 的前
的前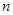 项和
项和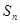
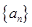 的前
的前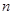 项和为
项和为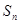 ,公差
,公差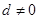 ,
,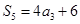 ,且
,且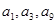 成等比数列.
成等比数列.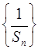 的前
的前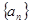 是等差数列,且
是等差数列,且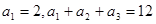
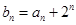 ,求数列
,求数列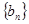 前n项和
前n项和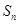 .
. 满足:
满足: ,
, .
. 及
及 ,求数列
,求数列 的前n项和
的前n项和 .
. 的等比数列,且1-a2是a1与1+a3的等比中项,前n项和为Sn;数列{bn}是等差数列,b1=8,其前n项和Tn满足Tn=n
的等比数列,且1-a2是a1与1+a3的等比中项,前n项和为Sn;数列{bn}是等差数列,b1=8,其前n项和Tn满足Tn=n ·bn+1(
·bn+1( +
+ +
+ + +
+ + 与
与