题目内容
【题目】(1)已知直线![]() 经过点
经过点![]() ,且与直线
,且与直线![]() 的夹角为
的夹角为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)已知![]() 中顶点
中顶点![]() 的平分线方程分别为
的平分线方程分别为![]() 和
和![]() .求
.求![]() 边所在的直线方程.
边所在的直线方程.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() .
.
【解析】
(1)先由![]() 的方程得到其倾斜角为
的方程得到其倾斜角为![]() ,再由题意得出直线
,再由题意得出直线![]() 的倾斜角为
的倾斜角为![]() 或
或![]() ,根据直线
,根据直线![]() 经过点
经过点![]() ,即可求出直线方程;
,即可求出直线方程;
(2)先由角平分线的性质,得到直线![]() 经过点
经过点![]() 关于直线
关于直线![]() 和
和![]() 对称的点,设这两个对称点为
对称的点,设这两个对称点为![]() ,
,![]() ,根据点关于直线对称,求出点的的坐标,得出所求直线斜率,进而可得出直线方程.
,根据点关于直线对称,求出点的的坐标,得出所求直线斜率,进而可得出直线方程.
(1)因为直线![]() 的斜率为
的斜率为![]() ,所以其倾斜角为
,所以其倾斜角为![]() ,
,
又直线![]() 与直线
与直线![]() 的夹角为
的夹角为![]() ,
,
所以直线![]() 的倾斜角为
的倾斜角为![]() 或
或![]() ,
,
当直线![]() 的倾斜角为
的倾斜角为![]() 时,直线
时,直线![]() 的斜率不存在,因为直线
的斜率不存在,因为直线![]() 过点
过点![]() 可得:直线
可得:直线![]() 的方程为
的方程为![]() ;
;
当直线![]() 的倾斜角为
的倾斜角为![]() 时,其斜率为
时,其斜率为![]() ,因为直线
,因为直线![]() 过点
过点![]() ,
,
所以直线![]() 的方程为
的方程为![]() ,即
,即![]() ;
;
故直线![]() 的方程为
的方程为![]() 或
或![]() ;
;
(2)由角平分线可知,直线![]() 经过点
经过点![]() 关于直线
关于直线![]() 和
和![]() 对称的点,
对称的点,
设这两个对称点为![]() ,
,![]() ,
,
由点![]() 与点
与点![]() 关于直线
关于直线![]() 对称可得:
对称可得:
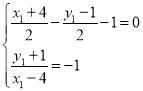 ,解得
,解得![]() ,即
,即![]() ;
;
由点![]() 与点
与点![]() 关于直线
关于直线![]() 对称可得:
对称可得:![]() ,
,![]()
所以![]() ;即
;即![]() ,
,
因此![]() 边所在的直线斜率为
边所在的直线斜率为![]() ,
,
因此![]() 边所在的直线方程为:
边所在的直线方程为:![]() ,即
,即![]() .
.

练习册系列答案
相关题目