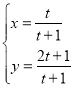题目内容
【题目】在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.已知曲线
轴正半轴为极轴建立极坐标系.已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),曲线
),曲线![]() 的极坐标方程为
的极坐标方程为![]() ,点
,点![]() 是
是![]() 与
与![]() 的一个交点,其极坐标为
的一个交点,其极坐标为![]() .设射线
.设射线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,与曲线
两点,与曲线![]() 相交于
相交于![]() ,
,![]() 两点.
两点.
(1)求![]() ,
,![]() 的值;
的值;
(2)求![]() 的最大值.
的最大值.
【答案】(1)![]() ;
;![]() (2)
(2)![]()
【解析】
(1)直接利用转换关系,把参数方程极坐标方程和直角坐标方程之间进行转换,进一步利用点的坐标求出结果.
(2)利用三角函数关系式的恒等变换和正弦型函数的性质的应用求出结果.
解:(1)将曲线![]() 的参数方程化成普通方程:
的参数方程化成普通方程:![]() ,
,
![]() 的直角坐标为
的直角坐标为![]() .
.
因为![]() 在
在![]() 上,所以
上,所以![]() ,解得
,解得![]() .
.
因为![]() 在
在![]() 上,所以
上,所以![]() ,解得
,解得![]() .
.
(2)曲线![]() 化为极坐标方程:
化为极坐标方程:![]() .
.
设![]() 的极坐标为
的极坐标为![]() ,
,![]() 的极坐标为
的极坐标为![]() ,则
,则![]() ,
,![]() .
.
因为![]() ,
,![]() 分别是
分别是![]() 与
与![]() ,
,![]() 的交点,所以
的交点,所以![]() .
.
所以
故![]() ,
,
其中![]() 为锐角,且
为锐角,且![]() .
.
因为![]() ,当
,当![]() 时等号成立.
时等号成立.
所以![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目