题目内容
某住宅小区有居民2万户,从中随机抽取200户,调查是否安装电话,调查的结果如表所示,则该小区已安装电话的户数估计有 ( )
| 电话 | 动迁户 | 原住户 |
| 已安装 | 65 | 30 |
| 未安装 | 40 | 65 |
C
解析试题分析：首先根据图表提供的数据算出200户居民中安装电话的频率，用总住户乘以频率即可．解：由图表可知，调查的200户居民中安装电话的有95户，所以安装电话的居民频率为95:200根据用户样本中已安装电话的频率得：20000×
=9500．所以该小区已安装电话的住户估计有9500（户）．故选C
考点：用样本的数字特征估计总体的数字特征
点评：本题考查了用样本的数字特征估计总体的数字特征，用样本的频率分布估计总体的分布，解答此类问题的关键是利用频率相等，是基础题
甲、乙两位歌手在“中国好声音”选拔赛中，5位评委评分情况如茎叶图所示，记甲、乙两人的平均得分分别为
、
，则下列判断正确的是（ ）
A． ，甲比乙成绩稳定 | B．，乙比甲成绩稳定 |
C． ，甲比乙成绩稳定 | D．，乙比甲成绩稳定 |
由一组数据(x1，y1)、(x2、y2)、 、(xn，yn)得到的线性回归方程为y＝a＋bx，则下列说法正确的是( )
A．直线y＝a＋bx必过点( ， ) |
| B．直线y＝a＋bx至少经过点(x1，y1)、(x2，y2)、 、(xn，yn)中的一点 |
| C．直线y＝a＋bx是由(x1，y1)、(x2、y2)、 、(xn，yn)中的两点确定的 |
| D．(x1，y1)、(x2，y2)、 、(xn、yn)这n个点到直线y＝a＋bx的距离之和最小 |
为了解某种轮胎的性能，随机抽取了8个进行测试，其最远里程数（单位：1000km）为：96, 112, 97, 108, 99, 104, 86, 98，则他们的中位数是( )
| A．100 | B．99 | C．98.5 | D．98 |
有一个容量为
的样本，其频率分布直方图如图所示，据图估计，样本数据在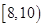
内的频数为
| A．38 | B．57 |
| C．76 | D．95 |
下图是甲、乙两名篮球运动员在以往几场篮球赛中得分的茎叶图，设
甲、乙两组数据的平均数分别为
，
，中位数分别为m甲，m乙，则
| A．<，m甲> m乙 | B．<，m甲< m乙 |
| C．，m甲> m乙 | D．>，m甲< m乙 |
工人月工资y（元）与劳动生产率x（千元）变化的回归方程
，下列判断正确的是 ( )
①劳动生产率为1千元时，工资约为130元
②劳动生产率提高1千元时，月工资约提高80元
③劳动生产率提高1千元时，月工资约提高130元
④当月工资为210元时，劳动生产率约为2千元
| A．① ② | B．① ② ④ | C．② ④ | D．① ② ③ ④ |
根据一组样本数据
的散点图分析存在线性相关关系，求得其回归方程
，则在样本点
处的残差为（ ）
A． | B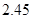． | C． | D． |
两个变量
与
的回归模型中，分别选择了4个不同模型，它们的相关指数
如下 ，其中拟合效果最好的模型是( )
| A．模型1的相关指数为0.98 | B．模型2的相关指数为0.80 |
| C．模型3的相关指数为0.50 | D．模型4的相关指数为0.25 |