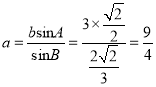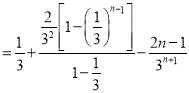题目内容
【题目】如图，四边形ABCD内接于⊙O，过点A作⊙O的切线EP交CB的延长线于P，∠PAB=35°． 
（1）若BC是⊙O的直径，求∠D的大小；
（2）若∠PAB=35°，求证： 
．
【答案】
（1）解：∵EP与⊙O相切于点A，∴∠ACB=∠PAB=35°，
又BC是⊙O的直径，∴∠ABC=55°．
∵四边形ABCD内接于⊙O，∴∠ABC+∠D=180°，
∴∠D=112°
（2）证明：∵∠DAE=35°，
∴∠ACD=∠PAB，∠D=∠PBA，
∴△ADC∽△ABP，
∴ 
= 
，∠DBA=∠BDA，
∴DA=BA，∴DA2=DCBP，AP2=PCBP，
∴ 
【解析】（1）由弦切角定理得∠ACB=∠PAB=25°，从而∠ABC=65°，由此利用四边形ABCD内接于⊙O，能求出∠D．（2）由∠DAE=25°，∠ACD=∠PAB，∠D=∠PBA，从而△ADC∽△PBA，由此能证明DA2=DCBP，AP2=PCBP，即可证明结论．
练习册系列答案
相关题目
