题目内容
设过抛物线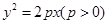
的焦点F的弦PQ，则以PQ为直径的圆与抛物线准线的位置关系是（ ）
A．相交 B．相切
C．相离 D．以上答案均有可能
【答案】
B
【解析】解：设PQ的中点是M，M到准线的距离是d．
而P到准线的距离d1=|PF|，Q到准线的距离d2=|QF|．
又M到准线的距离d是梯形的中位线，故有d=(|PF|+|QF| )/2 =|PQ| /2 ．
即圆心M到准线的距离等于半径|PQ|/ 2 ，
所以圆与准线是相切．
故选B．
练习册系列答案
相关题目