题目内容
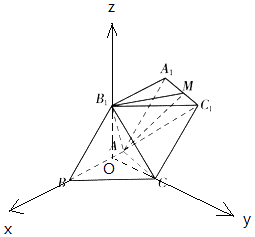
【题目】如图,已知斜三棱柱ABC﹣A1B1C1的所有棱长均为2,∠B1BA= ![]() ,且侧面ABB1A1⊥底面ABC. (Ⅰ)证明:B1C⊥AC1
,且侧面ABB1A1⊥底面ABC. (Ⅰ)证明:B1C⊥AC1
(Ⅱ)若M为A1C1的中点,求二面角A﹣B1M﹣A1的余弦值.
【答案】(Ⅰ)证明:过B1作BO⊥平面ABC, ∵斜三棱柱ABC﹣A1B1C1的所有棱长均为2,∠B1BA= ![]() ,
,
M,N分别为A1C1与B1C的中点,且侧面ABB1A1⊥底面ABC.
∴△ABC和△ABB1是边长为2的等边三角形,∴O是AB中点,∴B1O= ![]() ,
,
∴OB,OB1 , OC两两垂直,
以O为原点,OB为x轴,OC为y轴,OB1为z轴,建立空间直角坐标系,
则O(0,0,0),B1(0,0, ![]() ),C(0,
),C(0, ![]() ,0),A(﹣1,0,0),C1(﹣1,
,0),A(﹣1,0,0),C1(﹣1, ![]() ,
, ![]() ),
),![]() =(0,
=(0, ![]() ),
), ![]() =(0,
=(0, ![]() ),
),
∴ ![]() =0+3﹣3=0,
=0+3﹣3=0,
∴B1C⊥AC1 .
(Ⅱ)解:∵M为A1C1的中点,A1(﹣2,0, ![]() ),A(﹣1,0,0),B1(0,0,
),A(﹣1,0,0),B1(0,0, ![]() ),C1(﹣1,
),C1(﹣1, ![]() ,
, ![]() ),M(﹣
),M(﹣ ![]() ,
, ![]() ,
, ![]() ),
),
∴ ![]() =(1,0,
=(1,0, ![]() ),
), ![]() =(﹣
=(﹣ ![]() ,
, ![]() ,
, ![]() ),
),
设平面AB1M的法向量 ![]() =(x,y,z),
=(x,y,z),
则 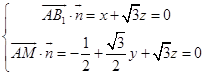 ,取z=1,得
,取z=1,得 ![]() =(﹣
=(﹣ ![]() ,3,1),
,3,1),
平面B1MA1的法向量 ![]() =(0,0,1),
=(0,0,1),
设二面角A﹣B1M﹣A1的平面角为θ,
则cosθ= ![]() =
= ![]() =
= ![]() .
.
∴二面角A﹣B1M﹣A1的余弦值为 ![]() .
.
【解析】(Ⅰ)过B1作BO⊥平面ABC,则OB,OB1 , OC两两垂直,以O为原点,OB为x轴,OC为y轴,OB1为z轴,建立空间直角坐标系,利用向量法能证明B1C⊥AC1 . (Ⅱ)求出平面AB1M的法向量和平面B1MA1的法向量,利用向量法能求出二面角A﹣B1M﹣A1的余弦值.
【考点精析】关于本题考查的直线与平面垂直的性质,需要了解垂直于同一个平面的两条直线平行才能得出正确答案.

【题目】某班主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查,统计数据如表所示:
积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性一般 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
(Ⅰ)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(Ⅱ)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关?并说明理由.
参考公式与临界值表:K2= ![]() .
.
p(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
【题目】某公司有A,B,C,D,E五辆汽车,其中A、B两辆汽车的车牌尾号均为1,C、D两辆汽车的车牌尾号均为2,E车的车牌尾号为6,已知在非限行日,每辆车可能出车或不出车,A、B、E三辆汽车每天出车的概率均为 ![]() ,C、D两辆汽车每天出车的概率均为
,C、D两辆汽车每天出车的概率均为 ![]() ,且五辆汽车是否出车相互独立,该公司所在地区汽车限行规定如下:
,且五辆汽车是否出车相互独立,该公司所在地区汽车限行规定如下:
车牌尾号 | 0和5 | 1和6 | 2和7 | 3和8 | 4和9 |
限行日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
(1)求该公司在星期一至少有2辆汽车出车的概率;
(2)设X表示该公司在星期二和星期三两天出车的车辆数之和,求X的分布列及数学期望.
