题目内容
抛物线 的准线与
的准线与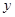 轴交于
轴交于 ,焦点为
,焦点为 ,若椭圆
,若椭圆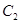 以
以 、
、 为焦点、且离心率为
为焦点、且离心率为 .
.
(1)当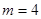 时,求椭圆
时,求椭圆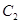 的方程;
的方程;
(2)若抛物线 与直线
与直线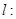
 及
及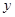 轴所围成的图形的面积为
轴所围成的图形的面积为 ,求抛物线
,求抛物线 和直线
和直线 的方程.
的方程.
 的准线与
的准线与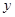 轴交于
轴交于 ,焦点为
,焦点为 ,若椭圆
,若椭圆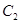 以
以 、
、 为焦点、且离心率为
为焦点、且离心率为 .
. (1)当
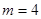 时,求椭圆
时,求椭圆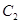 的方程;
的方程;(2)若抛物线
 与直线
与直线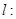
 及
及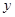 轴所围成的图形的面积为
轴所围成的图形的面积为 ,求抛物线
,求抛物线 和直线
和直线 的方程.
的方程.(1)
(2) 抛物线方程为 ,直线方程为
,直线方程为

(2) 抛物线方程为
 ,直线方程为
,直线方程为
试题分析:解:(1)当
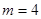 时,抛物线
时,抛物线 的准线为
的准线为 ,
,则
 , 2分
, 2分设椭圆
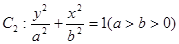 ,则
,则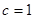 ,离心率
,离心率 4分 故
4分 故 ,
, 此时椭圆
此时椭圆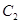 的方程为
的方程为 6分
6分(2)由
 消
消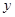 得:
得: ,解得
,解得 8分
8分故所围成的图形的面积
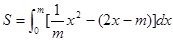
 10分
10分解得:
 ,又
,又 ,
, ,
,所以:抛物线方程为
 ,直线方程为
,直线方程为 12分
12分点评:解决的关键是熟悉圆锥曲线方程和性质,以及利用定积分表示曲边梯形面积的运用,属于中档题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
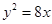 的焦点为右焦点,且经过点A(2,3).
的焦点为右焦点,且经过点A(2,3).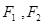 分别为椭圆的左右焦点,求
分别为椭圆的左右焦点,求 的角平分线所在直线的方程.
的角平分线所在直线的方程. 的一般方程式为
的一般方程式为
 ,设P、Q分别为曲线C1与曲线C2上的任意一点,求|PQ|的最小值
,设P、Q分别为曲线C1与曲线C2上的任意一点,求|PQ|的最小值 焦点的直线交抛物线于A、B两点,则
焦点的直线交抛物线于A、B两点,则 的最小值为
的最小值为  B.
B.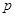 C.
C. D.无法确定
D.无法确定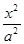 +
+ =1(a>b>0)的左、右焦点分别为F
=1(a>b>0)的左、右焦点分别为F 、F
、F ,A是椭圆C上的一点,AF
,A是椭圆C上的一点,AF
 +y
+y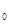 ,y
,y +
+ =1.(m<6) 与
=1.(m<6) 与 +
+ =1.(5<m<9)的( )
=1.(5<m<9)的( ) 和-1,则点C所对应的实数是
和-1,则点C所对应的实数是

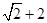

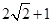
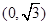 ,曲线C的参数方程为
,曲线C的参数方程为 (φ为参数)。以原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
(φ为参数)。以原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为 。
。 的值。
的值。