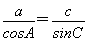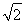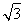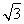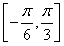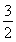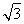题目内容
在△ABC中,A、B、C所对的边分别是a、b、c,且bcosB是acosC、ccosA的等差中项.
(1)求B的大小;
(2)若a+c=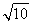 ,b=2,求△ABC的面积.
,b=2,求△ABC的面积.
(1)B=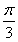 (2)
(2)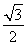
【解析】(1)由题意,得acosC+ccosA=2bcosB.由正弦定理,得sinAcosC+cosAsinC=2sinBcosB,
即sin(A+C)=2sinBcosB.
∵A+C=π-B,0<B<π,∴sin(A+C)=sinB≠0.∴cosB=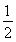 ,∴B=
,∴B=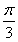 .
.
(2)由B=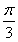 ,得
,得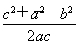 =
=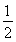 ,即
,即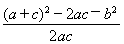 =
=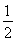 ,∴ac=2.
,∴ac=2.
∴S△ABC=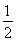 acsinB=
acsinB=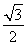 .
.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目