Question

过双曲线x²-y²=1的右焦点9作直线l交双曲线于A、B两点，记双曲线渐近线的方向向量为v，当在v方向上的投影的绝对值为时，求直线l的方程．

Answer 1

解：由已知，F(，0)，双曲线的渐近线y=±x的方向向量为v=(1，±1)，

当l斜率不存在时，不失一般性，取A(，-1)、B(，1)，则在v上的投影的绝对值为||cos45°=2，不合题意．

所以l的斜率k存在，其方程为y=k(x-)．

由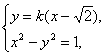得

(k²-1)x²-2k²x+2k²+1=0(k²≠1)

设A[x₁，k(x_l-)]、B[x₂，k(x₂-)]，

则x_l+x₂=,x₁x₂=．

当v=(1，1)时，设与v的夹角为θ，则

=[x₂-x₁，k(x₂-x₁)]在v上投影的绝对值

|||cosθ|=||

=

=

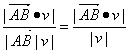
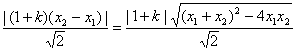
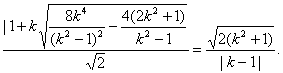
由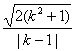=，得2k²-5k+2=0，k=2或k=

根据双曲线的对称性知，当

v=(1，-1)时，k=-2或k=-.

所以直线l的方程为y=±2 (x-)或y=±(x-).