题目内容
过双曲线x2-y2=8的右焦点F2的一条弦PQ,|PQ|=7,F1是左焦点,那么△F1PQ的周长为( )
分析:根据双曲线方程得a=b=2
,c=4.由双曲线的定义,证出|PF1|+|QF1|=|PF2|+|QF2|+8
=|PQ|+8
,结合
|PQ|=7即可算出△F1PQ的周长.
| 2 |
| 2 |
| 2 |
|PQ|=7即可算出△F1PQ的周长.
解答:解:∵双曲线方程为x2-y2=8,
∴a=b=2
,c=4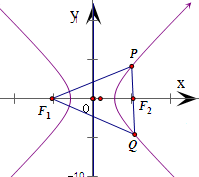
根据双曲线的定义,得
|PF1|-|PF2|=4
,|QF1|-|QF2|=4
,
∴|PF1|=|PF2|+4
,|QF1|=(|QF2|+4
),
相加可得|PF1|+|QF1|=|PF2|+|QF2|+8
,
∵|PF2|+|QF2|=|PQ|=7,∴|PF1|+|QF1|=7+8
,
因此△F1PQ的周长=|PF1|+|QF1|+|PQ|=7+8
+7=14+8
,
故选:C
∴a=b=2
| 2 |

根据双曲线的定义,得
|PF1|-|PF2|=4
| 2 |
| 2 |
∴|PF1|=|PF2|+4
| 2 |
| 2 |
相加可得|PF1|+|QF1|=|PF2|+|QF2|+8
| 2 |
∵|PF2|+|QF2|=|PQ|=7,∴|PF1|+|QF1|=7+8
| 2 |
因此△F1PQ的周长=|PF1|+|QF1|+|PQ|=7+8
| 2 |
| 2 |
故选:C
点评:本题给出经过双曲线右焦点的弦PQ长,求PQ与左焦点构成三角形的周长,着重考查了双曲线的标准方程、定义与简单几何性质等知识,属于基础题.

练习册系列答案
相关题目