题目内容
若曲线f(x)=ax2+lnx存在垂直于y轴的切线,则实数a的取值范围是 .
(-∞,0)
【思路点拨】求出导函数,根据导函数有零点,求a的取值范围.
解:由题意知该函数的定义域为(0,+∞),且f'(x)=2ax+
.因为存在垂直于y轴的切线,故此时斜率为0,问题转化为x>0时导函数f'(x)=2ax+存在零点的问题.
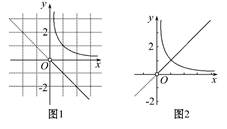
方法一(图象法):将之转化为g(x)=-2ax与h(x)=存在交点.
当a=0时不符合题意,当a>0时,如图1,数形结合可得没有交点,当a<0时,如图2,此时正好有一个交点,故有a<0,应填(-∞,0).
方法二(分离变量法):可等价于方程2ax+=0在(0,+∞)内有解,显然可得a=-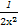
∈(-∞,0).
解:由题意知该函数的定义域为(0,+∞),且f'(x)=2ax+
.因为存在垂直于y轴的切线,故此时斜率为0,问题转化为x>0时导函数f'(x)=2ax+存在零点的问题.方法一(图象法):将之转化为g(x)=-2ax与h(x)=
存在交点.当a=0时不符合题意,当a>0时,如图1,数形结合可得没有交点,当a<0时,如图2,此时正好有一个交点,故有a<0,应填(-∞,0).
方法二(分离变量法):可等价于方程2ax+
=0在(0,+∞)内有解,显然可得a=-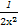∈(-∞,0).
练习册系列答案
相关题目
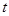的函数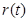
，若球的体积以均匀速度
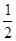增长，则球的表面积的增长速度与球半径的乘积为 .
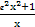,g(x)=
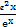,对任意x1,x2∈(0,+∞),不等式
≤
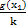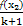恒成立,则正数k的取值范围是 .
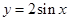的导数
