题目内容
函数f(x)=x3+bx2+cx+d在区间[-2,2]上是减函数,则b+c的最大值为 .
-12
由题意知f'(x)=3x2+2bx+c在区间[-2,2]上满足f'(x)≤0恒成立,
即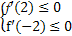
⇒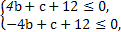 此问题相当于在约束条件
此问题相当于在约束条件
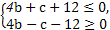 下,求目标函数z=b+c的最大值,由于
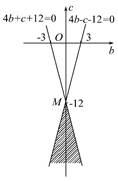
下,求目标函数z=b+c的最大值,由于 ⇒M(0,-12),如图可知,当直线l:b+c=z过点M时,z最大,所以过M点时值最大为-12.
⇒M(0,-12),如图可知,当直线l:b+c=z过点M时,z最大,所以过M点时值最大为-12.
即
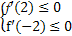
⇒
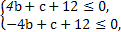 此问题相当于在约束条件
此问题相当于在约束条件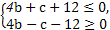 下,求目标函数z=b+c的最大值,由于
下,求目标函数z=b+c的最大值,由于 ⇒M(0,-12),如图可知,当直线l:b+c=z过点M时,z最大,所以过M点时值最大为-12.
⇒M(0,-12),如图可知,当直线l:b+c=z过点M时,z最大,所以过M点时值最大为-12.

练习册系列答案
相关题目
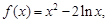
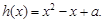
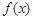 的极值;
的极值;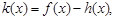 若函数
若函数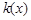 在
在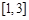 上恰有两个不同零点,求实数
上恰有两个不同零点,求实数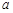 的取值范围.
的取值范围.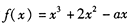 .对于任意实数x恒有
.对于任意实数x恒有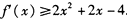
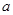 的最大值;
的最大值;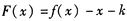 有三个零点,求实数k的取值范围。
有三个零点,求实数k的取值范围。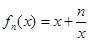 ,(
,(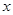 >0,
>0,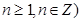 ,以点
,以点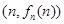 为切点作函数
为切点作函数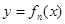 图象的切线
图象的切线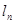 ,记函数
,记函数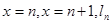 所围成的区域面积为
所围成的区域面积为 .
.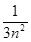 ;
;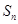 为数列
为数列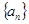 的前
的前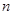 项和,求证:
项和,求证: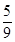 .来
.来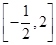 上只有一个零点,求实数a的取值范围.
上只有一个零点,求实数a的取值范围.