题目内容
已知函数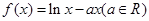
(Ⅰ) 求函数 的单调区间;
的单调区间;
(Ⅱ) 当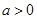 时,求函数
时,求函数 在
在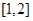 上的最小值.
上的最小值.
(Ⅰ)详见解析;(Ⅱ)详见解析.
解析试题分析:(Ⅰ)一般来说,判断函数的单调区间,就要考察函数的导函数在此区间上的符号,本题中,由于函数中含有参数,这就可能引起分类讨论;(Ⅱ)求函数在某区间上的最值,一般仍是先考察函数在此区间上的单调性,再求其最值,本题中的参数是引起分类讨论的原因,难度较大,分类时要层次清晰,数形结合的思想的应用能迅速帮助找到分类的标准.
试题解析:(Ⅰ)  , 1分
, 1分
①当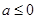 时,
时,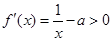 ,
,
故函数 增函数,即函数
增函数,即函数 的单调增区间为
的单调增区间为 . 3分
. 3分
②当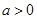 时,令
时,令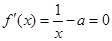 ,可得
,可得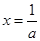 ,
,
当 时,
时,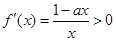 ;当
;当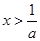 时,
时, ,
,
故函数 的单调递增区间为
的单调递增区间为 ,单调减区间是
,单调减区间是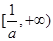 6分
6分
(Ⅱ) 由(Ⅰ)知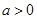 时,函数
时,函数 的单调递增区间为
的单调递增区间为 ,单调减区间是
,单调减区间是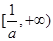
①当 ,即
,即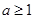 时,函数
时,函数 在区间
在区间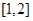 上是减函数,
上是减函数,
∴ 的最小值是
的最小值是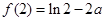 . 7分
. 7分
②当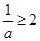 ,即
,即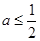 时,函数
时,函数 在区间
在区间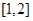 上是增函数,
上是增函数,
∴ 的最小值是
的最小值是 . 9分
. 9分
③当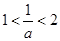 ,即
,即 时,函数
时,函数 在
在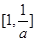 上是增函数,在
上是增函数,在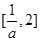 是减函数.
是减函数.
又 ,∴当
,∴当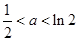 时,最小值是
时,最小值是 ;
;
当 时,最小值为
时,最小值为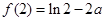 . 11分
. 11分
综上可知,当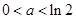 时, 函数
时, 函数 的最小值是
的最小值是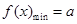 ;当
;当 时,函数
时,函数 的最小值是
的最小值是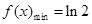 12分
12分
考点:函数的单调性、导数的应用.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 ,函数
,函数 .
. 时,写出函数
时,写出函数 的单调递增区间;
的单调递增区间; 时,求函数
时,求函数 ,函数
,函数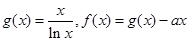 .
.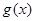 的单调区间;
的单调区间; 在区间
在区间 上是减函数,求实数
上是减函数,求实数 的最小值;
的最小值;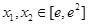 (
(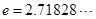 是自然对数的底数)使
是自然对数的底数)使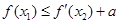 ,求实数
,求实数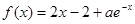 (
(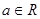 )
) 在点
在点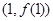 处的切线平行于
处的切线平行于 轴,求
轴,求 的值;
的值;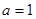 时,若直线
时,若直线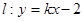 与曲线
与曲线 上有公共点,求
上有公共点,求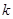 的取值范围.
的取值范围.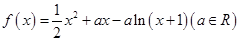 .
.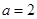 时,求函数
时,求函数 的极值;
的极值; ,使函数
,使函数 在
在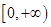 上有唯一的零点,若有,请求出
上有唯一的零点,若有,请求出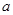 的范围;若没有,请说明理由.
的范围;若没有,请说明理由.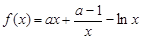
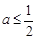 时,试讨论函数
时,试讨论函数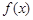 的单调性;
的单调性;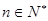 ,有
,有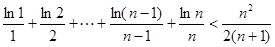 .
.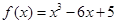 ,
,
 的单调区间;
的单调区间;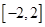 上的最值.
上的最值.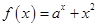 ,
,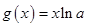 ,
,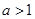 .
.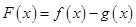 在
在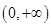 上单调递增;
上单调递增;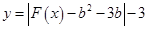 有四个零点,求
有四个零点,求 的取值范围.
的取值范围.
 时,求
时,求 的极值;
的极值;  上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围.