Question

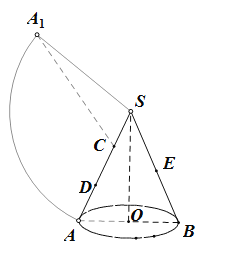
【题目】在意大利，有一座满是“斗笠”的灰白小镇阿尔贝罗贝洛（Alberobello），这些圆锥形屋顶的奇特小屋名叫Trullo，于1996年被收入世界文化遗产名录（如图1）.现测量一个屋顶，得到圆锥SO的底面直径AB长为12m，母线SA长为18m（如图2）.C，D是母线SA的两个三等分点（点D靠近点A），E是母线SB的中点.

（1）从点A到点C绕屋顶侧面一周安装灯光带，求灯光带的最小长度；

（2）现对屋顶进行加固，在底面直径AB上某一点P，向点D和点E分别引直线型钢管PD和PE.试确定点P的位置，使得钢管总长度最小.

Answer 1

【答案】（1）；（2）时，的最小值为

【解析】

（1）将侧面沿母线展开，点对于与，连接，则为最小长度，在中由余弦定理计算可得.

（2）建立平面直角坐标系，求出关于轴的对称点，利用两点间的距离公式求出距离最小值，利用点斜式求出直线方程，即可求出的坐标.

解：（1）将侧面沿母线展开，点对于与，连接，则为最小长度；

因为，，则，设

，，

在中由余弦定理可得

即

即灯光带的最小长度为（）

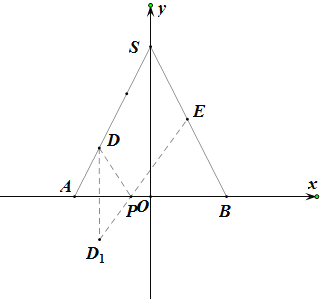
（2）如图建立平面直角坐标系，因为，

所以，，，因为是的三等分点（靠近）

所以，又是的中点，所以

则关于轴对称的点为

连接与轴交点，则的最小值为

直线的方程为

令则

即时，的最小值为