题目内容
【题目】已知函数f(x)=lnx﹣x2+ax,a∈R.
(Ⅰ)证明lnx≤x﹣1;
(Ⅱ)若a≥1,讨论函数f(x)的零点个数.
【答案】(Ⅰ)见解析(Ⅱ)见解析
【解析】
(Ⅰ)令![]() 进而求导求最值即可证得;
进而求导求最值即可证得;
(Ⅱ)求函数导数,分析单调性,由f(1>0,![]() 及
及![]() ,利用零点存在定理即可得解.
,利用零点存在定理即可得解.
(Ⅰ)证明:令![]() ,
,
可得:x∈(0,1)时,g′(x)>0,函数g(x)单调递增;x∈(1,+∞)时,g′(x)<0,函数g(x)单调递减.
∴可得x=1时,函数g(x)取得极大值即最大值,∴g(x)≤g(1)=0,即lnx≤x﹣1.
(II)解:根据题意,![]() .
.
令![]() ,解得
,解得![]() ,(负值舍去),
,(负值舍去),
在(0,x0)上,![]() ,函数f(x)单调递增;在(x0,+∞)上,
,函数f(x)单调递增;在(x0,+∞)上,![]() ,函数f(x)单调递减.
,函数f(x)单调递减.
∴f(x)max=f(x0).
当a=1时,x0=1,f(x)max=f(1)=0,此时函数f(x)只有一个零点1.
当a>1时,![]() ,f(1)=a﹣1>0,
,f(1)=a﹣1>0,![]() .
.
![]() .
.
∴函数f(x)在区间![]() 和区间(1,2a)上各有一个零点.
和区间(1,2a)上各有一个零点.
综上可得:当a=1时,函数f(x)只有一个零点1.
当a>1时,函数f(x)有两个零点.

【题目】为了解某校学生参加社区服务的情况,采用按性别分层抽样的方法进行调查.已知该校共有学生960人,其中男生560人,从全校学生中抽取了容量为![]() 的样本,得到一周参加社区服务的时间的统计数据好下表:
的样本,得到一周参加社区服务的时间的统计数据好下表:
超过1小时 | 不超过1小时 | |
男 | 20 | 8 |
女 | 12 | m |
(Ⅰ)求![]() ,
,![]() ;
;
(Ⅱ)能否有95%的把握认为该校学生一周参加社区服务时间是否超过1小时与性别有关?
(Ⅲ)以样本中学生参加社区服务时间超过1小时的频率作为该事件发生的概率,现从该校学生中随机调查6名学生,试估计6名学生中一周参加社区服务时间超过1小时的人数.
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]()
【题目】某公司为了提高利润,从2014年至2018年每年对生产环节的改进进行投资,投资金额与年利润增长的数据如下表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
投资金额x(万元) | 5 | 5.5 | 6 | 6.5 | 7 |
年利润增长y(万元) | 7.5 | 8 | 9 | 10 | 11.5 |
(1)请用最小二乘法求出y关于x的回归直线方程;
(2)如果2020年该公司计划对生产环节的改进的投资金额为8万元,估计该公司在该年的年利润增长为多少?
参考公式: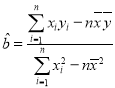 ,
,![]() 参考数据:
参考数据:![]() ,
,![]()