题目内容
【题目】已知函数![]() (
(![]() ),若不等式
),若不等式![]() 对任意实数
对任意实数![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】D
【解析】
根据题意,分析可得函数f(x)为奇函数且为增函数,进而可以将原问题转化为m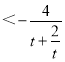 对任意实数t≥1恒成立,由基本不等式的性质分析可得
对任意实数t≥1恒成立,由基本不等式的性质分析可得![]() 有最小值
有最小值![]() ,进而分析可得m的取值范围.
,进而分析可得m的取值范围.
根据题意,函数f(x)=x3+3x,其定义域为R,关于原点对称,
有f(﹣x)=﹣(x3+3x)=﹣f(x),则f(x)为奇函数,
又由f′(x)=3x2+3>0,则f(x)为增函数,
若不等式f(2m+mt2)+f(4t)<0对任意实数t≥1恒成立,
则f(2m+mt2)<﹣f(4t),即2m+mt2<﹣4t对任意实数t≥1恒成立,
2m+mt2<﹣4tm![]() ,即m
,即m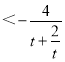 ,
,
又由t≥1,则t![]() 2
2![]() ,则
,则![]() 有最小值
有最小值![]() ,当且仅当
,当且仅当![]() 时等号成立
时等号成立
若m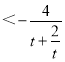 对任意实数t≥1恒成立,必有m
对任意实数t≥1恒成立,必有m![]() ;
;
即m的取值范围为(﹣∞,![]() );
);
故选:D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目