题目内容
(本小题满分l2分)
已知函数 (
(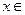 R ).
R ).
(Ⅰ)求函数 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
(Ⅱ)
 内角
内角 的对边长分别为
的对边长分别为 ,若
,若
 且
且 试判断
试判断
 的形状,并说明理由.
的形状,并说明理由.
已知函数
 (
(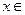 R ).
R ).(Ⅰ)求函数
 的最小正周期及单调递增区间;
的最小正周期及单调递增区间; (Ⅱ)

 内角
内角 的对边长分别为
的对边长分别为 ,若
,若
 且
且 试判断
试判断
 的形状,并说明理由.
的形状,并说明理由.解:(Ⅰ)∵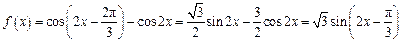 ,
,
∴.故函数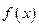 的最小正周期为
的最小正周期为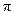 ;递增区间为
;递增区间为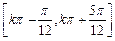 (
(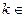 Z )………6分
Z )………6分
(Ⅱ)解法一: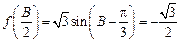 ,∴
,∴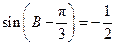 .
.
∵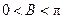 ,∴
,∴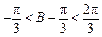 ,∴
,∴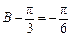 ,即
,即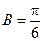 .……………………9分
.……………………9分
由余弦定理得: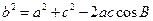 ,∴
,∴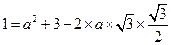 ,即
,即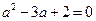 ,
,
故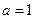 (不合题意,舍)或
(不合题意,舍)或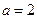 .……………………………11分
.……………………………11分
因为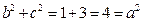 ,所以
,所以 ABC为直角三角形.………………………12分
ABC为直角三角形.………………………12分
解法二: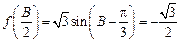 ,∴
,∴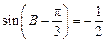 .
.
∵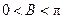 ,∴
,∴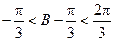 ,∴
,∴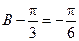 ,即
,即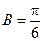 .…………………9分
.…………………9分
由正弦定理得: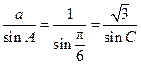 ,∴
,∴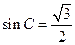 ,
,
∵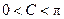 ,∴
,∴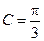 或
或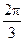 .
.
当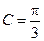 时,
时,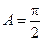 ;当
;当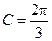 时,
时,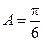 .(不合题意,舍) ………11分
.(不合题意,舍) ………11分
所以 ABC为直角三角形. ………12分
ABC为直角三角形. ………12分
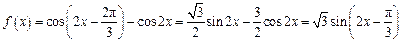 ,
,∴.故函数
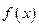 的最小正周期为
的最小正周期为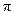 ;递增区间为
;递增区间为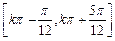 (
(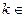 Z )………6分
Z )………6分(Ⅱ)解法一:
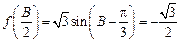 ,∴
,∴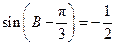 .
.∵
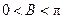 ,∴
,∴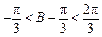 ,∴
,∴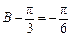 ,即
,即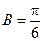 .……………………9分
.……………………9分由余弦定理得:
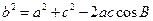 ,∴
,∴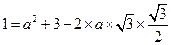 ,即
,即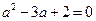 ,
,故
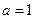 (不合题意,舍)或
(不合题意,舍)或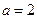 .……………………………11分
.……………………………11分因为
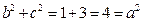 ,所以
,所以 ABC为直角三角形.………………………12分
ABC为直角三角形.………………………12分解法二:
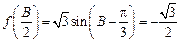 ,∴
,∴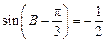 .
.∵
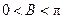 ,∴
,∴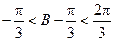 ,∴
,∴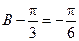 ,即
,即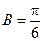 .…………………9分
.…………………9分由正弦定理得:
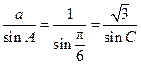 ,∴
,∴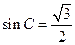 ,
,∵
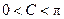 ,∴
,∴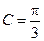 或
或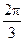 .
.当
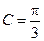 时,
时,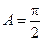 ;当
;当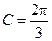 时,
时,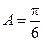 .(不合题意,舍) ………11分
.(不合题意,舍) ………11分所以
 ABC为直角三角形. ………12分
ABC为直角三角形. ………12分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
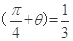 ,则
,则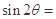 ( )
( )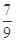
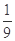
 (ω>0)在区间
(ω>0)在区间 上单调递增,在区间
上单调递增,在区间 上单调递减,则ω=
上单调递减,则ω=

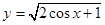 的定义域是 ( )
的定义域是 ( )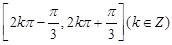
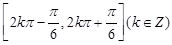
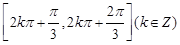
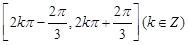
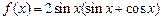 .
.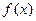 的最小正周期;
的最小正周期;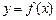 的单调递减区间
的单调递减区间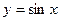 的图象经过怎样的变换得到?
的图象经过怎样的变换得到?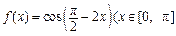 )的单调减区间为 .
)的单调减区间为 . ,下列结论中正确的是( )
,下列结论中正确的是( )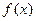 的最小正周期为
的最小正周期为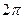 ;
;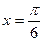 对称;
对称;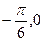 )对称;
)对称;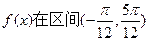 内是增函数.
内是增函数. 有零点,则m的取值范围( ▲ )
有零点,则m的取值范围( ▲ )

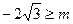 或
或

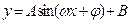 ,
,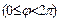 ,则温度变化曲线的函数解析式为 ▲ .
,则温度变化曲线的函数解析式为 ▲ . 