题目内容
设sin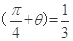 ,则
,则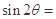 ( )
( )
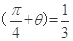 ,则
,则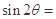 ( )
( )A.-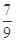 | B.-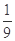 | C.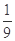 | D.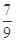 |
A
考点:
分析:利用两角和的正弦公式可得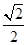 sinθ+
sinθ+ 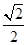 cosθ=
cosθ= 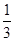 ,平方可得
,平方可得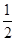 +
+ 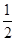 sin2θ=
sin2θ= 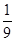 ,由此解得 sin2θ的值.
,由此解得 sin2θ的值.
解答:解:∵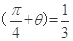 ,即
,即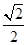 sinθ+
sinθ+ 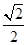 cosθ=
cosθ= 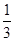 ,平方可得
,平方可得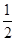 +
+ 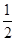 sin2θ=
sin2θ= 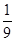 ,解得 sin2θ=-
,解得 sin2θ=-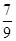 ,
,
故答案为-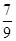 .
.
点评:本题主要考查两角和的正弦公式、二倍角的正弦的应用,属于基础题.
分析:利用两角和的正弦公式可得
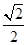 sinθ+
sinθ+ 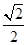 cosθ=
cosθ= 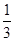 ,平方可得
,平方可得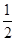 +
+ 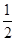 sin2θ=
sin2θ= 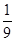 ,由此解得 sin2θ的值.
,由此解得 sin2θ的值.解答:解:∵
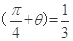 ,即
,即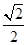 sinθ+
sinθ+ 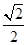 cosθ=
cosθ= 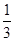 ,平方可得
,平方可得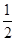 +
+ 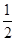 sin2θ=
sin2θ= 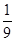 ,解得 sin2θ=-
,解得 sin2θ=-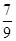 ,
,故答案为-
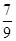 .
.点评:本题主要考查两角和的正弦公式、二倍角的正弦的应用,属于基础题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目

 (
( R)满足
R)满足 ,
, ,则函数
,则函数



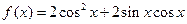 ,求:
,求: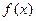 的最小正周期;(Ⅱ)
的最小正周期;(Ⅱ)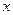 .
.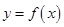 的图象沿
的图象沿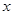 轴向左平移
轴向左平移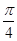 个单位,然后再把图象上每个点的横坐标伸长到原来的2倍(纵坐标保持不变),得到函数
个单位,然后再把图象上每个点的横坐标伸长到原来的2倍(纵坐标保持不变),得到函数 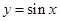 的图象,则
的图象,则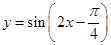
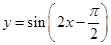
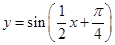
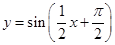
 (
(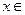 R ).
R ). 的最小正周期及单调递增区间;
的最小正周期及单调递增区间; 
 内角
内角 的对边长分别为
的对边长分别为 ,若
,若
 且
且 试判断
试判断 题:①存在实数α,使sinαcosα=1成立; ②存在实数α,使sinα+cosα=
题:①存在实数α,使sinαcosα=1成立; ②存在实数α,使sinα+cosα=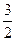 成立; ③函数
成立; ③函数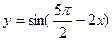 是偶函数; ④方程
是偶函数; ④方程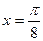 是函数
是函数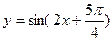 的图象的一条对称轴方程;⑤若α.β是第一象限角,且α>β,则tgα>tgβ。其中正确命题的序号是__________________
的图象的一条对称轴方程;⑤若α.β是第一象限角,且α>β,则tgα>tgβ。其中正确命题的序号是__________________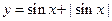 的值域 ( )
的值域 ( )