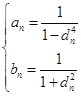题目内容
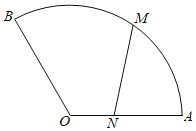
【题目】如图，空间几何体由两部分构成，上部是一个底面半径为1，高为2的圆锥，下部是一个底面半径为1，高为2的圆柱，圆锥和圆柱的轴在同一直线上，圆锥的下底面与圆柱的上底面重合，点
是圆锥的顶点，
是圆柱下底面的一条直径，
、
是圆柱的两条母线，
是弧的中点.
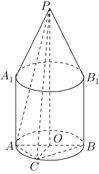
（1）求异面直线
与
所成的角的大小；
（2）求点
到平面
的距离.
【答案】（1）
；（2）
.
【解析】
（1）以
为原点，
为
轴，
为
轴，
为
轴，建立空间直角坐标系，利用向量法求出异面直线
与
所成的角的大小即可
（2）求出平面
的法向量，利用向量法求出点
到平面的距离
（1）由题意以为原点，为轴，为轴，为轴，建立空间直角坐标系，
如图
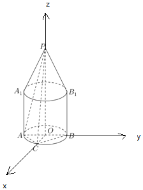
则
，
， 
，
，
， 
，
，
异面直线与所成的角的大小为．
（2）
， 
， 
， 
， 
，
设平面的法向量
，则
，取
，得
，
点到平面的距离为：
．
练习册系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
【题目】某工厂因排污比较严重，决定着手整治，一个月时污染度为
，整治后前四个月的污染度如下表：
月数 |
|
|
|
| … |
污染度 |
|
|
|
| … |
污染度为
后，该工厂即停止整治，污染度又开始上升，现用下列三个函数模拟从整治后第一个月开始工厂的污染模式：
，
，
，其中
表示月数，
、
、
分别表示污染度．
（1）问选用哪个函数模拟比较合理，并说明理由；
（2）若以比较合理的模拟函数预测，整治后有多少个月的污染度不超过![](http://thumb.zyjl.cn/questionBank/Upload/2020/05/31/06/c7ade7a2/SYS202005310600492128280640_ST/SYS202005310600492128280640_ST.001.png"){kind=small}
．
