题目内容
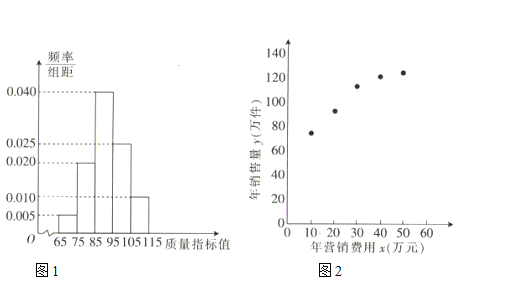
【题目】某企业生产一种产品,从流水线上随机抽取![]() 件产品,统计其质量指标值并绘制频率分布直方图(如图1):规定产品的质量指标值在
件产品,统计其质量指标值并绘制频率分布直方图(如图1):规定产品的质量指标值在![]() 的为劣质品,在
的为劣质品,在![]() 的为优等品,在
的为优等品,在![]() 的为特优品,销售时劣质品每件亏损
的为特优品,销售时劣质品每件亏损![]() 元,优等品每件盈利
元,优等品每件盈利![]() 元,特优品每件盈利
元,特优品每件盈利![]() 元,以这
元,以这![]() 件产品的质量指标值位于各区间的频率代替产品的质量指标值位于该区间的概率.
件产品的质量指标值位于各区间的频率代替产品的质量指标值位于该区间的概率.
(1)求每件产品的平均销售利润;
(2)该企业主管部门为了解企业年营销费用![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:万件)的影响,对该企业近
(单位:万件)的影响,对该企业近![]() 年的年营销费用
年的年营销费用![]() 和年销售量
和年销售量![]() ,
,![]() 数据做了初步处理,得到的散点图(如图2)及一些统计量的值.
数据做了初步处理,得到的散点图(如图2)及一些统计量的值.
|
|
|
|
|
|
|
|
表中![]() ,
,![]() ,
,![]() ,
,![]() .
.
根据散点图判断,![]() 可以作为年销售量
可以作为年销售量![]() (万件)关于年营销费用
(万件)关于年营销费用![]() (万元)的回归方程.
(万元)的回归方程.
①求![]() 关于
关于![]() 的回归方程;
的回归方程;
②用所求的回归方程估计该企业每年应投入多少营销费,才能使得该企业的年收益的预报值达到最大?(收益![]() 销售利润
销售利润![]() 营销费用,取
营销费用,取![]() )
)
附:对于一组数据![]() ,
,![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为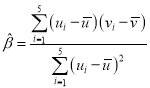 ,
,![]() .
.
【答案】(1)![]() 元.(2)①
元.(2)①![]() ②
②![]() 万元
万元
【解析】
(1)每件产品的销售利润为![]() ,由已知可得
,由已知可得![]() 的取值,由频率分布直方图可得劣质品、优等品、特优品的概率,从而可得
的取值,由频率分布直方图可得劣质品、优等品、特优品的概率,从而可得![]() 的概率分布列,依期望公式计算出期望即为平均销售利润;
的概率分布列,依期望公式计算出期望即为平均销售利润;
(2)①对![]() 取自然对数,得
取自然对数,得![]() ,
,
令![]() ,
,![]() ,
,![]() ,则
,则![]() ,这就是线性回归方程,由所给公式数据计算出系数,得线性回归方程,从而可求得
,这就是线性回归方程,由所给公式数据计算出系数,得线性回归方程,从而可求得![]() ;
;
②求出收益![]() ,可设
,可设![]() 换元后用导数求出最大值.
换元后用导数求出最大值.
解:(1)设每件产品的销售利润为![]() ,则
,则![]() 的可能取值为
的可能取值为![]() ,
,![]() ,
,![]() .由频率分布直方图可得产品为劣质品、优等品、特优品的概率分别为
.由频率分布直方图可得产品为劣质品、优等品、特优品的概率分别为![]() 、
、![]() 、
、![]() .
.
所以![]() ;
;![]() ;
;![]() .所以
.所以![]() 的分布列为
的分布列为
|
|
|
|
|
|
|
|
所以![]() (元).
(元).
即每件产品的平均销售利润为![]() 元.
元.
(2)①由![]() ,得
,得![]() ,
,
令![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,
由表中数据可得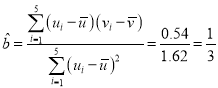 ,
,
则![]() ,
,
所以![]() ,即
,即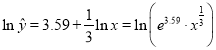 ,
,
因为取![]() ,所以
,所以![]() ,故所求的回归方程为
,故所求的回归方程为![]() .
.
②设年收益为![]() 万元,则
万元,则![]()
令![]() ,则
,则![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,所以当
,所以当![]() ,即
,即![]() 时,
时,![]() 有最大值
有最大值![]() .
.
即该企业每年应该投入![]() 万元营销费,能使得该企业的年收益的预报值达到最大,最大收益为
万元营销费,能使得该企业的年收益的预报值达到最大,最大收益为![]() 万元.
万元.

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案【题目】“绿水青山就是金山银山”,为了响应国家政策,我市环保部门对市民进行了一次环境保护知识的网络问卷调查,每位市民仅有一次参加机会,通过随机抽样,得到参与问卷调查的50人的得分(满分:100分)数据,统计结果如表所示:
组别 |
|
|
|
|
|
|
男 | 1 | 2 | 2 | 10 | 9 | 6 |
女 | 0 | 5 | 5 | 5 | 3 | 2 |
若规定问卷得分不低于70分的市民称为“环境保护关注者”,则上图中表格可得![]() 列联表如下:
列联表如下:
非“环境保护关注者” | 是“环境保护关注者” | 合计 | |
男 | 5 | 25 | 30 |
女 | 10 | 10 | 20 |
合计 | 15 | 35 | 50 |
(1)请完成上述![]() 列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“环境保护关注者”与性别有关?
列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“环境保护关注者”与性别有关?
(2)若问卷得分不低于80分的人称为“环境保护达人”,现在从本次调查的“环境保护达人”中利用分层抽样的方法抽取4名市民参与环保知识问答,再从这4名市民中随机抽取2人参与座谈会,求抽取的2名市民中,既有男“环境保护达人”又有女“环境保护达人”的概率.
附表及公式: ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |