题目内容
【题目】已知曲线
的极坐标方程是
,以极点为原点，以极轴为
轴的正半轴，取相同的单位长度，建立平面直角坐标系，直线
的参数方程为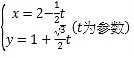
.
（1）写出直线的普通方程与曲线的直角坐标方程；
（2）设曲线经过伸缩变换
得到曲线
，曲线上任一点为
，求
的取值范围．
【答案】（1） 直线
的普通方程为
，曲线
的直角坐标方程为
.
（2）
的取值范围是
.
【解析】
试题（Ⅰ）利用
，将
转化成直角坐标方程，利用消参法法去直线参数方程中的参数
，得到直线的普通方程；（Ⅱ）根据伸缩变换公式求出变换后的曲线方程，然后利用参数方程表示出曲线上任意一点，代入，根据三角函数的辅助角公式求出其范围即可．
试题解析：（Ⅰ）直线的普通方程
曲线的直角坐标方程为
（Ⅱ）曲线经过伸缩变换
得到曲线
的方程为
，即
又点
在曲线上，则
（
为参数）
代入，得
所以的取值范围是
．
练习册系列答案
相关题目
【题目】高考复习经过二轮“见多识广”之后，为了研究考前“限时抢分”强化训练次数
与答题正确率
﹪的关系，对某校高三某班学生进行了关注统计，得到如下数据：
| 1 | 2 | 3 | 4 |
| 20 | 30 | 50 | 60 |
（1）求
关于
的线性回归方程，并预测答题正确率是100﹪的强化训练次数；
（2）若用
表示统计数据的“强化均值”（精确到整数），若“强化均值”的标准差在区间
内，则强化训练有效，请问这个班的强化训练是否有效？
附：回归直线的斜率和截距的最小二乘法估计公式分别为：
＝
， 
＝
－
，
样本数据
的标准差为： 
