题目内容
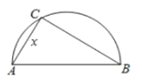
【题目】为美化环境,某市计划在以![]() 、
、![]() 两地为直径的半圆弧
两地为直径的半圆弧![]() 上选择一点
上选择一点![]() 建造垃圾处理厂(如图所示).已知
建造垃圾处理厂(如图所示).已知![]() 、
、![]() 两地的距离为
两地的距离为![]() ,垃圾场对某地的影响度与其到该地的距离有关,对
,垃圾场对某地的影响度与其到该地的距离有关,对![]() 、
、![]() 两地的总影响度对
两地的总影响度对![]() 地的影响度和对
地的影响度和对![]() 地影响度的和.记
地影响度的和.记![]() 点到
点到![]() 地的距离为
地的距离为![]() ,垃圾处理厂对
,垃圾处理厂对![]() 、
、![]() 两地的总影响度为
两地的总影响度为![]() .统计调查表明:垃圾处理厂对
.统计调查表明:垃圾处理厂对![]() 地的影响度与其到
地的影响度与其到![]() 地距离的平方成反比,比例系数为
地距离的平方成反比,比例系数为![]() ;对
;对![]() 地的影响度与其到
地的影响度与其到![]() 地的距离的平方成反比,比例系数为
地的距离的平方成反比,比例系数为![]() .当垃圾处理厂建在弧
.当垃圾处理厂建在弧![]() 的中点时,对
的中点时,对![]() 、
、![]() 两地的总影响度为
两地的总影响度为![]() .
.

(1)将![]() 表示成
表示成![]() 的函数;
的函数;
(2)判断弧![]() 上是否存在一点,使建在此处的垃圾处理厂对
上是否存在一点,使建在此处的垃圾处理厂对![]() 、
、![]() 两地的总影响度最小?若存在,求出该点到
两地的总影响度最小?若存在,求出该点到![]() 地的距离;若不存在,说明理由.
地的距离;若不存在,说明理由.
【答案】(1)![]() .
.
(2)当![]() 点到
点到![]() 点的距离为
点的距离为![]() 时,垃圾处理厂对两地的总影响度最小.
时,垃圾处理厂对两地的总影响度最小.
【解析】
(1)根据题意建立含参数![]() 的函数解析式,将
的函数解析式,将![]() 时
时![]() 代入,求得
代入,求得![]() ,即可求得函数解析式;
,即可求得函数解析式;
(2)利用导数,确定函数的单调性及最值,即可求得答案.
解:(1)由题意![]() ,
,![]() ,
,
则![]() ,
,
其中,当![]() 时,
时,![]() ,故
,故![]() ,
,
∴![]() .
.
(2)存在.由(1)可得![]()
![]() ,
,
令![]() 得
得![]() ,
,
当![]() 时,
时,![]() ,故函数在区间
,故函数在区间![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,故函数在区间
,故函数在区间![]() 单调递增,
单调递增,
故![]() 时,函数有最小值.
时,函数有最小值.
即当![]() 点到
点到![]() 点的距离为
点的距离为![]() 时,垃圾处理厂对两地的总影响度最小.
时,垃圾处理厂对两地的总影响度最小.
(另解:此问也可用基本不等式求最值)

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案【题目】某中学为了解高一年级学生身高发育情况,对全校![]() 名高一年级学生按性别进行分层抽样检查,测得身高(单位:
名高一年级学生按性别进行分层抽样检查,测得身高(单位:![]() )频数分布表如表
)频数分布表如表![]() 、表
、表![]() .
.
表![]() :男生身高频数分布表
:男生身高频数分布表
身高/ |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
表![]() :女生身高频数分布表
:女生身高频数分布表
身高/ |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
(1)求该校高一女生的人数;
(2)估计该校学生身高在![]() 的概率;
的概率;
(3)以样本频率为概率,现从高一年级的男生和女生中分别选出![]() 人,设
人,设![]() 表示身高在
表示身高在![]() 学生的人数,求
学生的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
【题目】某地随着经济的发展,居民收入逐年增长,下表是该地一建设银行连续五年的储蓄存款(年底余额),如下表1:
年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
储蓄存款y (千亿元) | 5 | 6 | 7 | 8 | 10 |
为了研究计算的方便,工作人员将上表的数据进行了处理,![]() 得到下表2:
得到下表2:
时间代号t | 1 | 2 | 3 | 4 | 5 |
z | 0 | 1 | 2 | 3 | 5 |
(1)求z关于t的线性回归方程;
(2)通过(1)中的方程,求出y关于x的回归方程;
(3)用所求回归方程预测到2020年年底,该地储蓄存款额可达多少?
(附:对于线性回归方程![]() ,其中
,其中 )
)
