题目内容
6.已知抛物线y2=2px(p>0),过点C(-2,0)的直线l交抛物线于A,B两点,坐标原点为O,$\overrightarrow{OA}$•$\overrightarrow{OB}$=12.(I)求抛物线的方程;
(Ⅱ)当以AB为直径的圆与y轴相切时,求直线l的方程.
分析 (Ⅰ)设l:x=my-2,代入y2=2px,可得根与系数的关系,再利用$\overrightarrow{OA}$•$\overrightarrow{OB}$=12,可得x1x2+y1y2=12,代入即可得出.
(Ⅱ)由(Ⅰ)(?)化为y2-4my+8=0.设AB的中点为M,可得|AB|=2xm=x1+x2=m(y1+y2)-4=4m2-4,又|AB|=$\sqrt{1+{m}^{2}}$|y1-y2|=$\sqrt{(1+{m}^{2})(16{m}^{2}-32)}$,联立解出m即可得出.
解答 解:(Ⅰ)设l:x=my-2,代入y2=2px,
可得y2-2pmy+4p=0.(?)
设A(x1,y1),B(x2,y2),
则y1+y2=2pm,y1y2=4p,
则x1x2=$\frac{{y}_{1}^{2}}{2p}•\frac{{y}_{2}^{2}}{2p}$=4.
∵$\overrightarrow{OA}$•$\overrightarrow{OB}$=12,
∴x1x2+y1y2=12,
即4+4p=12,
得p=2,抛物线的方程为y2=4x.
(Ⅱ)由(Ⅰ)(?)化为y2-4my+8=0.
y1+y2=4m,y1y2=8.
设AB的中点为M,
则|AB|=2xm=x1+x2=m(y1+y2)-4=4m2-4,①
又|AB|=$\sqrt{1+{m}^{2}}$|y1-y2|=$\sqrt{(1+{m}^{2})(16{m}^{2}-32)}$,②
由①②得(1+m2)(16m2-32)=(4m2-4)2,
解得m2=3,m=±$\sqrt{3}$.
∴直线l的方程为x+$\sqrt{3}$y+2=0,或x-$\sqrt{3}$y+2=0.
点评 本题考查了抛物线的标准方程及其性质、直线与抛物线相交问题转化为方程联立可得根与系数的关系、焦点弦长公式、弦长公式、直线与圆相切的性质、数量积运算,考查了推理能力与计算能力,属于中档题.

| A. | x±2y=0 | B. | 2x±y=0 | C. | $\sqrt{3}$x±y=0 | D. | x$±\sqrt{3}$y=0 |
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 2 | D. | $\sqrt{2}$ |
 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点 如图,四边形ABCD为菱形,MA⊥平面ABCD,四边形ADNM是平行四边形.
如图,四边形ABCD为菱形,MA⊥平面ABCD,四边形ADNM是平行四边形.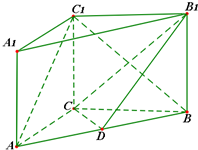 如图,在直三棱柱ABC-A1B1C1中,点D是AB的中点,BC=CC1=4,AB=10,CD=3.
如图,在直三棱柱ABC-A1B1C1中,点D是AB的中点,BC=CC1=4,AB=10,CD=3.