题目内容

11．圆（x-r）2+y2=r2（r＞0），点M在圆上，O为原点，以∠MOx=φ为参数，那么圆的参数方程为$\left\{\begin{array}{l}{x=r+r•cos2φ}\\{y=r•sin2φ}\end{array}\right.$ （φ为参数）．

分析 由题意可得圆心C（r，0），半径为r，且∠MCx=2φ．设点M（x，y），则根据x=r+rcos2φ，y=rsin2φ，求得此圆的参数方程．

解答 解：由题意可得圆心C（r，0），半径为r，且∠MCx=2φ．
设点M（x，y），则x=r+rcos2φ，y=rsin2φ，
故圆的参数方程为$\left\{\begin{array}{l}{x=r+r•cos2φ}\\{y=r•sin2φ}\end{array}\right.$ （φ为参数），
故答案为：$\left\{\begin{array}{l}{x=r+r•cos2φ}\\{y=r•sin2φ}\end{array}\right.$ （φ为参数）．

点评 本题主要考查圆的参数方程的求法，属于基础题．

练习册系列答案
相关题目
1．设函数f（x）=ax2+bx+1（a、b∈R），F（x）=$\left\{\begin{array}{l}{f（x），x＞0}\\{-f（x），x＜0}\end{array}\right.$．
（1）若f（-1）=0，且对任意实数x均有f（x）≥0成立，求F（x）的表达式；
（2）在（1）的条件下，当x∈[-2，2]时，g（x）=f（x）-kx是单调函数，求实数k的取值范围；
（3）设m＞0，n＜0，且m+n＞0，a＞0，f（x）为偶函数，求证：F（m）+F（n）＞0．
2．有四个命题：
（1）z1，z2∈C⇒$\overline{{z}_{1}}$•z2+z1•$\overline{{z}_{2}}$∈R；
（2）z1，z2∈C，z12+z22=0⇒z1=z2=0；
（3）z1-z2=0⇒z1与z2互为共轭复数；
（4）z+$\overline{z}$=0⇒z为纯虚数．
上述命题正确的是（　　）
A．（1）（2）B．（2）（3）C．（3）（4）D．（1）（3）
19．已知函数f（x）=lg$\frac{1+{2}^{x}+a•{3}^{x}}{3}$．
（1）若f（x）的定义域为（-∞，1），求a的值；
（2）若f（x）在x∈（-∞，1）内恒有意义，求a的取值范围．
6．函数y=cos$\frac{πx}{3}$的值域是[-1，1]．
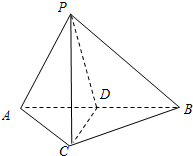2．如图，在三棱锥P-ABC中，AC=BC=2，∠ACB=90°，AP=BP=AB，PC⊥AC．
（Ⅰ）求证：PC⊥AB；
（Ⅱ）求二面角B-AP-C的大小的余弦；
（Ⅲ）求点C到平面APB的距离．
9．已知函数f（x）=lnx+$\frac{m}{x}$，m∈R，
（1）若曲线y=f（x）在点（1，f（1））处的切线与y轴交点的纵坐标为1，求m；
（2）讨论f（x）的单调性；
（3）若对任意b＞a＞0，$\frac{f（b）-f（a）}{b-a}$＜1恒成立，求m的取值范围．
6．已知抛物线y2=2px（p＞0），过点C（-2，0）的直线l交抛物线于A，B两点，坐标原点为O，$\overrightarrow{OA}$•$\overrightarrow{OB}$=12．
（I）求抛物线的方程；
（Ⅱ）当以AB为直径的圆与y轴相切时，求直线l的方程．
7．已知函数f（x）=ax2+x|x-b|．
（Ⅰ）当b=-1时，若不等式f（x）≥-2x-1恒成立．求实数a的最小值；
（Ⅱ）若a＜0，且对任意b∈[1，2]，总存在实数m，使得方程|f（x）-m|=$\frac{1}{4}$在[-3，3]上有6个互不相同的解，求实数a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网