Question

15．如图，在直三棱柱ABC-A₁B₁C₁中，点D是AB的中点，BC=CC₁=4，AB=10，CD=3．
（Ⅰ）求证：AC₁∥面CDB₁；
（Ⅱ）求证：C₁B⊥面CDB₁．

Answer 1

分析 （Ⅰ）连结C₁B与CB₁交于点O，再连结OD，只要证明AC₁∥OD，利用线面平行的判定定理可得；
（Ⅱ）利用线面垂直的判定定理，只要证明CD⊥C₁B和C₁B⊥B₁C，即可．

解答 解：（Ⅰ）证明：连结C₁B与CB₁交于点O，再连结OD，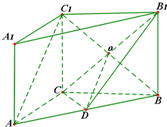

∵AC₁∥OD，OD?面B₁CD，AC₁?面B₁CD
∴AC₁∥面B₁CD…（6分）
（Ⅱ）证明：在直三棱柱ABC-A₁B₁C₁中CC₁⊥面ABC∴CC₁⊥CD…（7分）
∵CD²+BC²=9+16=25=BD²
∴CD⊥BC．…（8分）
又∵CC₁∩BC=C，…（9分）
∴CD⊥面C₁BC．…（10分）
∵C₁B?面C₁BC，∴CD⊥C₁B．
又∵CC₁=CB，
∴CBB₁C₁为矩形，
∴C₁B⊥B₁C
又CB₁∩CD=C，
所以C₁B⊥面CDB₁…（13分）

点评 本题考查了线面平行的判定和线面垂直的判定定理的运用；关键是熟练运用定理的条件．