题目内容
4.已知函数f(x)=logax+x-b(其中2<a<3<b<4),函数f(x)的零点x0∈(n,n+1),n∈N*,则n的值为( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 把要求零点的函数,变成两个基本初等函数,根据所给的a,b的值,可以判断两个函数的交点的所在的位置,同所给的区间进行比较,得到n的值.
解答 解:设函数y=logax,y=-x+b
根据2<a<3<b<4,
对于函数y=logax,当x=2时,函数值y<1,当x=3时,函数值y>1,
在同一坐标系中划出两个函数的图象,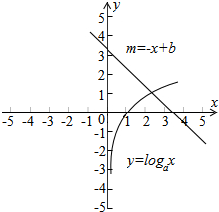
判断两个函数的图形的交点在(2,3)之间,
∴函数f(x)的零点x0∈(n,n+1)时,n=2,
故选:C
点评 本题考查函数零点的判定定理,是一个基本初等函数的图象的应用,这种问题一般应用数形结合思想来解决.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
14. 如图,直线x=a,x=a+1(a>0),y=x2及x轴围成的曲线梯形面积介于相应小矩形与大矩形面积之间,即a2<${∫}_{a}^{a+1}$x2dx<(a+1)2.类比之,?n∈N*,$\frac{1}{n+1}$+$\frac{1}{n+2}$+…+$\frac{1}{2n}$<A<$\frac{1}{n}+\frac{1}{n+1}$+…+$\frac{1}{2n-1}$恒成立,求实数A等于( )
如图,直线x=a,x=a+1(a>0),y=x2及x轴围成的曲线梯形面积介于相应小矩形与大矩形面积之间,即a2<${∫}_{a}^{a+1}$x2dx<(a+1)2.类比之,?n∈N*,$\frac{1}{n+1}$+$\frac{1}{n+2}$+…+$\frac{1}{2n}$<A<$\frac{1}{n}+\frac{1}{n+1}$+…+$\frac{1}{2n-1}$恒成立,求实数A等于( )
 如图,直线x=a,x=a+1(a>0),y=x2及x轴围成的曲线梯形面积介于相应小矩形与大矩形面积之间,即a2<${∫}_{a}^{a+1}$x2dx<(a+1)2.类比之,?n∈N*,$\frac{1}{n+1}$+$\frac{1}{n+2}$+…+$\frac{1}{2n}$<A<$\frac{1}{n}+\frac{1}{n+1}$+…+$\frac{1}{2n-1}$恒成立,求实数A等于( )
如图,直线x=a,x=a+1(a>0),y=x2及x轴围成的曲线梯形面积介于相应小矩形与大矩形面积之间,即a2<${∫}_{a}^{a+1}$x2dx<(a+1)2.类比之,?n∈N*,$\frac{1}{n+1}$+$\frac{1}{n+2}$+…+$\frac{1}{2n}$<A<$\frac{1}{n}+\frac{1}{n+1}$+…+$\frac{1}{2n-1}$恒成立,求实数A等于( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{5}$ | C. | ln2 | D. | ln$\frac{5}{2}$ |
15.$\frac{{C}_{11}^{1}{+C}_{11}^{3}{+C}_{11}^{5}+…{+C}_{11}^{11}}{{3}^{11}-{{3}^{10}{C}_{11}^{1}+{3}^{9}{C}_{11}^{2}+{3}^{8}{C}_{11}^{3}+…+3{C}_{11}^{10}-1}$等于( )
| A. | -1 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
9.已知向量$\overrightarrow{a}$=(1,-2,2),$\overrightarrow{b}$=(2,-1,2),那么向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角等于( )
| A. | -arccos$\frac{8}{9}$ | B. | π-arccos$\frac{8}{9}$ | C. | arccos$\frac{8}{9}$ | D. | π+arccos$\frac{8}{9}$ |
16.从3名高一学生,3名高二学生和5名高三学生中选派4人参加座谈会,则三个年级都至少有1人参加的选派方法有( )种.
| A. | 90 | B. | 150 | C. | 180 | D. | 210 |