题目内容
【题目】一盒中装有9张各写有一个数字的卡片，其中4张卡片上数字是1，3张卡片上数字是2，2张卡片上数字是3.从盒中任取3张卡片.
(1)求所取3张卡片上数字完全相同的概率；
(2)已知取出的一张卡片上数字是1，求3张卡片上数字之和为5的概率.
【答案】(1)
(2)
.
【解析】
（1）根据组合数分别求总事件数与所取3张卡片上数字完全相同事件数，再根据古典概型概率公式求结果，（2）求条件概率，先求满足条件取出3张卡片，一张卡片上数字是1的概率，再求“一张卡片上数字是1且3张卡片上数字之和为5”的概率，再根据条件概率公式得结果.
(1)设“所取3张卡片上数字完全相同”为事件A，则P(A)=
=
(2)设B表示“取出3张卡片，一张卡片上数字是1”，C表示“3张卡片上数字之和为5”.
(方法1)P(B)=
=
，P(BC)=
=
，
所以P(C|B)=
=
(方法2)P(C|B)=
=
=.
【题目】假设关于某种设备的使用年限
(年)与所支出的维修费用
(万元)有如下统计资料：
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
已知
， 
.
， 
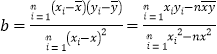(1)求
， 
；
(2)若 与具有线性相关关系，求出线性回归方程；
(3)估计使用年限为10年时，维修费用约是多少？
【题目】一则“清华大学要求从 2017级学生开始，游泳达到一定标准才能毕业”的消息在体育界和教育界引起了巨大反响.其实，已有不少高校将游泳列为必修内容.
某中学拟在高一-下学期开设游泳选修课，为了了解高--学生喜欢游泳是否与性别有关，该学校对100名高一新生进行了问卷调查，得到如下
列联表:
喜欢游泳 | 不喜欢游泳 | 合计 | |
男生 | 40 | ||
女生 | 30 | ||
合计 |
已知在这100人中随机抽取1人，抽到喜欢游泳的学生的概率为
.
(1).请将上述列联表补充完整，并判断是否可以在犯错误的概率不超过0.001的前提下认为喜欢游泳与性别有关.
(2)已知在被调查的学生中有6名来自高一(1) 班，其中4名喜欢游泳，现从这6名学生中随机抽取2人，求恰有1人喜欢游泳的概率.
附：
| 0.10 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 /td> | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
