题目内容
(2012•黄州区模拟)(考生注意:本题为选做题,请在下列两题中任选一题作答,如果都做,则按所做第(1)题计分)
(1)(《坐标系与参数方程选讲》选做题).已知曲线C的极坐标方程为ρ=2cosθ,则曲线C上的点到直线
(t为参数)距离的最大值为

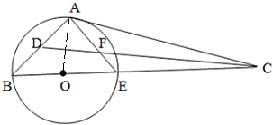
(2)(《几何证明选讲》选做题).已知点C在圆O的直径BE的延长线上,直线CA与圆O相切于点A,∠ACB的平分线分别交AB,AE于点D,F,则∠ADF
(1)(《坐标系与参数方程选讲》选做题).已知曲线C的极坐标方程为ρ=2cosθ,则曲线C上的点到直线
|
1+
4
| ||
| 5 |
1+
.4
| ||
| 5 |

(2)(《几何证明选讲》选做题).已知点C在圆O的直径BE的延长线上,直线CA与圆O相切于点A,∠ACB的平分线分别交AB,AE于点D,F,则∠ADF
45°
45°
.分析:(1)将曲线C方程化成普通方程,可得曲线C表示以C(1,0)为圆心,半径为1的圆.可得曲线C上的点到直线距离的最大值等于圆心到直线的距离加上圆的半径,由此结合点到直线距离公式,则不难求出这个最大值.
(2)连接AO,根据切线的性质定理,得∠ACB+∠AOC=90°,再用等腰三角形底角相等和三角形外角定理,结合CD平分∠ACB,可得∠ADF=∠DCB+∠B=
(∠AOC+∠ACB)=45°.
(2)连接AO,根据切线的性质定理,得∠ACB+∠AOC=90°,再用等腰三角形底角相等和三角形外角定理,结合CD平分∠ACB,可得∠ADF=∠DCB+∠B=
| 1 |
| 2 |
解答:解:(1)曲线C的极坐标方程为ρ=2cosθ,化成直角坐标得x2+y2-2x=0
∴曲线C表示以C(1,0)为圆心,半径为1的圆
直线
(t为参数)化成普通方程,得2x-y+2=0
可得点C到直线的距离为:d=
=
∴曲线C上的点到直线的距离的最大值为1+
(2)连接AO,
∵AC与l圆O相切于点A,∴OA⊥AC,可得∠ACB+∠AOC=90°
∵OA=OB,∴∠B=∠BAO=
∠AOC
又∵CD平分∠ACB,∴∠DCB=
∠ACB
因此,∠ADF=∠DCB+∠B=
(∠AOC+∠ACB)=45°
故答案为:1+
45°
∴曲线C表示以C(1,0)为圆心,半径为1的圆
直线
|
可得点C到直线的距离为:d=
| |2-0+2| | ||
|
4
| ||
| 5 |

∴曲线C上的点到直线的距离的最大值为1+
4
| ||
| 5 |
(2)连接AO,
∵AC与l圆O相切于点A,∴OA⊥AC,可得∠ACB+∠AOC=90°
∵OA=OB,∴∠B=∠BAO=
| 1 |
| 2 |
又∵CD平分∠ACB,∴∠DCB=
| 1 |
| 2 |
因此,∠ADF=∠DCB+∠B=
| 1 |
| 2 |
故答案为:1+
4
| ||
| 5 |
点评:本题第一小问给出圆上动点,求该点到直线距离的最大值,考查了极坐标、参数方程与普通方程的互化和点到直线距离公式等知识,第二小问已经圆的直径和切线,求一个角的大小,着重考查了三角形外角定理、等边对等角和切线的性质等知识,两题都属于基础题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
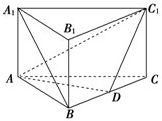 (2012•黄州区模拟)如图,在直三棱柱ABC-A1B1C1中,AB=BC=2AA1,∠ABC=90°,D是BC的中点.
(2012•黄州区模拟)如图,在直三棱柱ABC-A1B1C1中,AB=BC=2AA1,∠ABC=90°,D是BC的中点. (2012•黄州区模拟)已知某几何体的三视图如图,则该几何体的表面积为
(2012•黄州区模拟)已知某几何体的三视图如图,则该几何体的表面积为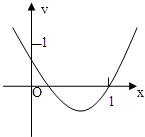 (2012•黄州区模拟)如图是二次函数f(x)=x2-bx+a的部分图象,则函数g(x)=2lnx+f(x)在点(b,g(b))处切线的斜率的最小值是( )
(2012•黄州区模拟)如图是二次函数f(x)=x2-bx+a的部分图象,则函数g(x)=2lnx+f(x)在点(b,g(b))处切线的斜率的最小值是( )