题目内容
【题目】如图，在平面直角坐标系xOy中，已知直线l：x
y2=0，抛物线C：y2=2px（p＞0）.
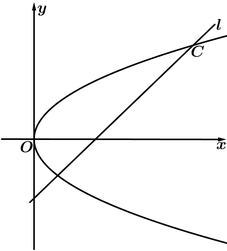
（1）若直线l过抛物线C的焦点，求抛物线C的方程；
（2）已知抛物线C上存在关于直线l对称的相异两点P和Q.
①求证：线段PQ的中点坐标为
；
②求p的取值范围.
【答案】（1）
；（2）①证明见解析;②
.
【解析】
（1）先确定抛物线焦点，再将点代入直线方程；（2）①利用抛物线点之间关系进行化简，结合中点坐标公式求证;②利用直线与抛物线位置关系确定数量关系：
，解出p的取值范围.
（1）抛物线
的焦点为
由点在直线
上，得
，即
所以抛物线C的方程为
（2）设
，线段PQ的中点
因为点P和Q关于直线
对称，所以直线垂直平分线段PQ，
于是直线PQ的斜率为
，则可设其方程为
①由
消去
得
因为P 和Q是抛物线C上的相异两点，所以
从而
，化简得
.
方程（*）的两根为
，从而
因为在直线上，所以
因此，线段PQ的中点坐标为
②因为
在直线
上
所以
，即
由①知，于是
，所以
因此
的取值范围为
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案【题目】下表提供了工厂技术改造后某种型号设备的使用年限x和所支出的维修费y（万元）的几组对照数据:
x（年） | 2 | 3 | 4 | 5 | 6 |
y（万元） | 1 | 2.5 | 3 | 4 | 4.5 |
（1）若知道y对x呈线性相关关系，请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程
；
（2）已知该工厂技术改造前该型号设备使用10年的维修费用为9万元，试根据（1）求出的线性回归方程，预测该型号设备技术改造后，使用10年的维修费用能否比技术改造前降低?参考公式: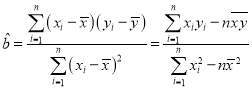
，
.
【题目】某公司对4月份员工的奖金情况统计如下：
奖金（单位：元） | 8000 | 5000 | 4000 | 2000 | 1000 | 800 | 700 | 600 | 500 |
员工（单位：人） | 1 | 2 | 4 | 6 | 12 | 8 | 20 | 5 | 2 |
根据上表中的数据，可得该公司4月份员工的奖金：①中位数为800元；②平均数为1373元；③众数为700元，其中判断正确的个数为（ ）
A.0B.1C.2D.3
