Question

【题目】设集合Pn={1，2，…，n}，n∈N* ． 记f（n）为同时满足下列条件的集合A的个数：
①APn；②若x∈A，则2xA；③若x∈ A，则2x A．
（1）求f（4）；
（2）求f（n）的解析式（用n表示）．

Answer 1

【答案】
（1）

解当n=4时，P4={1，2，3，4}，符合条件的集合A为：{2}，{1，4}，{2，3}，{1，3，4}

故f（4）=4

（2）

解：任取偶数x∈pn，将x除以2，若商仍为偶数，再除以2…，经过k次后，商必为奇数，此时记商为m，

于是x=m2k，其中m为奇数，k∈N*

由条件可知，若m∈A，则x∈A，k为偶数

若mA，则x∈Ak为奇数

于是x是否属于A由m是否属于A确定，设Qn是Pn中所有的奇数的集合

因此f（n）等于Qn的子集个数，当n为偶数时（或奇数时），Pn中奇数的个数是 （或 ）

∴

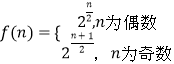
【解析】（1）由题意可得P4={1，2，3，4}，符合条件的集合A为：{2}，{1，4}，{2，3}，{1，3，4}，故可求f（4）（2）任取偶数x∈pn ， 将x除以2，若商仍为偶数，再除以2…，经过k次后，商必为奇数，此时记商为m，可知，若m∈A，则x∈A，k为偶数；若mA，则x∈Ak为奇数，可求
【考点精析】本题主要考查了元素与集合关系的判断的相关知识点，需要掌握对象与集合的关系是，或者，两者必居其一才能正确解答此题．