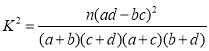题目内容
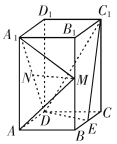
【题目】如图,在四棱锥P-ABCD中,![]() 是等腰三角形,且
是等腰三角形,且![]() .四边形ABCD是直角梯形,
.四边形ABCD是直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
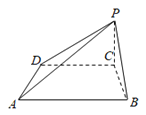
(1)求证:![]() 平面PDC.
平面PDC.
(2)请在图中所给的五个点P,A,B,C,D中找出两个点,使得这两点所在直线与直线BC垂直,并给出证明.
(3)当平面![]() 平面ABCD时,求直线PC与平面PAB所成角的正弦值.
平面ABCD时,求直线PC与平面PAB所成角的正弦值.
【答案】(1)详见解答;(2)![]() ,证明见解答;(3)
,证明见解答;(3)![]() .
.
【解析】
(1)由已知![]() ,即可证明结论;
,即可证明结论;
(2)根据已知条件排除![]() ,只有
,只有![]() 可能与
可能与![]() 垂直,根据已知可证
垂直,根据已知可证![]() ;
;
(3)利用垂直关系,建立空间直角坐标系,求出![]() 坐标和平面PAB的法向量,即可求解.
坐标和平面PAB的法向量,即可求解.
(1)![]() 平面
平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ;
;
(2)![]() ,证明如下:
,证明如下:
取![]() 中点
中点![]() ,连
,连![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() ;
;
(3)平面![]() 平面ABCD,平面
平面ABCD,平面![]() 平面ABCD
平面ABCD![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,
,
.四边形ABCD是直角梯形,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]()
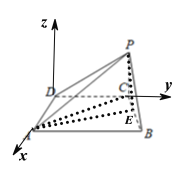
以![]() 为坐标原点,以
为坐标原点,以![]() ,过
,过![]() 点与
点与![]() 平行的直线分别为
平行的直线分别为![]() 轴,
轴,
建立空间直角坐标系![]() ,则
,则![]() ,
,
![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则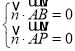 ,即
,即![]() ,
,
![]() ,令
,令![]() ,则
,则![]() ,
,
平面![]() 一个法向量为
一个法向量为![]() ,
,
设直线PC与平面PAB所成角为![]() ,
,
![]() ,
,
直线直线PC与平面PAB所成角的正弦值为![]() .
.

【题目】2019年上半年我国多个省市暴发了“非洲猪瘟”疫情,生猪大量病死,存栏量急剧下降,一时间猪肉价格暴涨,其他肉类价格也跟着大幅上扬,严重影响了居民的生活.为了解决这个问题,我国政府一方面鼓励有条件的企业和散户防控疫情,扩大生产;另一方面积极向多个国家开放猪肉进口,扩大肉源,确保市场供给稳定.某大型生猪生产企业分析当前市场形势,决定响应政府号召,扩大生产决策层调阅了该企业过去生产相关数据,就“一天中一头猪的平均成本与生猪存栏数量之间的关系”进行研究.现相关数据统计如下表:
生猪存栏数量 | 2 | 3 | 4 | 5 | 8 |
头猪每天平均成本 | 3.2 | 2.4 | 2 | 1.9 | 1.5 |
(1)研究员甲根据以上数据认为![]() 与
与![]() 具有线性回归关系,请帮他求出
具有线性回归关系,请帮他求出![]() 关于
关于![]() 的线.性回归方程
的线.性回归方程![]() (保留小数点后两位有效数字)
(保留小数点后两位有效数字)
(2)研究员乙根据以上数据得出![]() 与
与![]() 的回归模型:
的回归模型:![]() .为了评价两种模型的拟合效果,请完成以下任务:
.为了评价两种模型的拟合效果,请完成以下任务:
①完成下表(计算结果精确到0.01元)(备注:![]() 称为相应于点
称为相应于点![]() 的残差);
的残差);
生猪存栏数量 | 2 | 3 | 4 | 5 | 8 | |
头猪每天平均成本 | 3.2 | 2.4 | 2 | 1.9 | 1.5 | |
模型甲 | 估计值 | |||||
残差 | ||||||
模型乙 | 估计值 | 3.2 | 2.4 | 2 | 1.76 | 1.4 |
残差 | 0 | 0 | 0 | 0.14 | 0.1 | |
②分别计算模型甲与模型乙的残差平方和![]() 及
及![]() ,并通过比较
,并通过比较![]() 的大小,判断哪个模型拟合效果更好.
的大小,判断哪个模型拟合效果更好.
(3)根据市场调查,生猪存栏数量达到1万头时,饲养一头猪每一天的平均收入为7.5元;生猪存栏数量达到1.2万头时,饲养一头猪每一天的平均收入为7.2元若按(2)中拟合效果较好的模型计算一天中一头猪的平均成本,问该生猪存栏数量选择1万头还是1.2万头能获得更多利润?请说明理由.(利润=收入-成本)
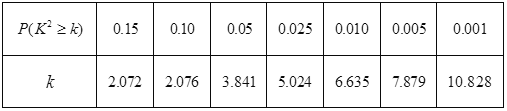
参考公式: .
.
参考数据:![]() .
.