题目内容
甲、乙、丙三人独立地对某一技术难题进行攻关。甲能攻克的概率为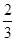 ,乙能攻克的概率为
,乙能攻克的概率为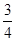 ,丙能攻克的概率为
,丙能攻克的概率为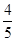 .
.
(1)求这一技术难题被攻克的概率;
(2)若该技术难题末被攻克,上级不做任何奖励;若该技术难题被攻克,上级会奖励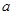 万元。奖励规则如下:若只有1人攻克,则此人获得全部奖金
万元。奖励规则如下:若只有1人攻克,则此人获得全部奖金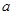 万元;若只有2人攻克,则奖金奖给此二人,每人各得
万元;若只有2人攻克,则奖金奖给此二人,每人各得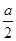 万元;若三人均攻克,则奖金奖给此三人,每人各得
万元;若三人均攻克,则奖金奖给此三人,每人各得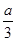 万元。设甲得到的奖金数为X,求X的分布列和数学期望。(本题满分12分)
万元。设甲得到的奖金数为X,求X的分布列和数学期望。(本题满分12分)
(1)这一技术难题被攻克的概率为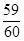 ;
;
(2 X的分布列为X 0 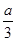
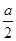
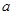
P 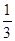
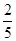
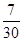

数学期望为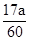 。
。
解析试题分析:(1) …………4分
…………4分
(2) 的可能取值分别为
的可能取值分别为 …………………5分
…………………5分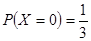 ,
, 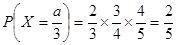 ,
, ,
,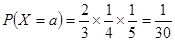 ,………………………9分
,………………………9分
∴ X的分布列为X 0 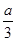
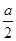
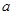
P 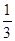
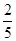
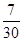

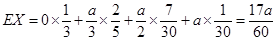 (万元) …………12分
(万元) …………12分
考点:本题考查等可能事件的概率;离散型随机变量的期望及其分布列。
点评:本题解题的关键是一别漏掉某种情况;二是数字的运算比较麻烦,需要认真计算,得到结果

练习册系列答案
相关题目
编号为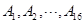 的16名篮球运动员在某次训练比赛中的得分记录如下:
的16名篮球运动员在某次训练比赛中的得分记录如下:
| 运动员编号 | 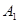 | 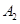 |  |  |  |  | 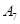 | 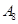 |
| 得分 | 15 | 35 | 21 | 28 | 25 | 36 | 18 | 34 |
| 运动员编号 | 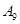 | 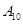 |  |  |  |  |  |  |
| 得分 | 17 | 26 | 25 | 33 | 22 | 12 | 31 | 38 |
(Ⅰ)将得分在对应区间内的人数填入相应的空格;
| 区间 |  | 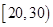 | 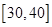 |
| 人数 | | | |
(Ⅱ)从得分在区间
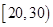 内的运动员中随机抽取2人,
内的运动员中随机抽取2人,(i)用运动员的编号列出所有可能的抽取结果;
(ii)求这2人得分之和大于50的概率.
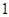 次,求在这一枪出现空弹的概率;
次,求在这一枪出现空弹的概率; 次,求在这三枪中出现空弹的概率;
次,求在这三枪中出现空弹的概率; 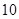 的等边
的等边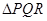 ,甲射手用实弹瞄准了三角形
,甲射手用实弹瞄准了三角形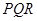 区域随机射击,且弹孔都落在三角形
区域随机射击,且弹孔都落在三角形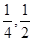 ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为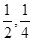 ;两人租车时间都不会超过四小时。
;两人租车时间都不会超过四小时。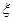 ,求
,求 .
.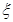 表示取出的3个小球上的最大数字,求:
表示取出的3个小球上的最大数字,求: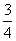 ,乙答对每个题的概率为
,乙答对每个题的概率为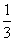 。
。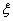 ,求
,求