题目内容

3．已知等差数列{an}共有10项，其奇数项之和为10，偶数项之和为30，则其公差是4．

分析 利用等差中项的性质可知5（a1+4d）=10、5（a1+5d）=30，计算即得结论．

解答 解：依题意，a1+（a1+2d）+（a1+4d）+（a1+6d）+（a1+8d）=5（a1+4d）=10，
同理，5（a1+5d）=30，
两式相减得：d=4，
故答案为：4．

点评 本题考查等差数列的性质，注意解题方法的积累，属于中档题．

练习册系列答案
相关题目
13．实数m为何值时，复数z=m2（$\frac{1}{m+5}$+i）+（8m+15）i+$\frac{m-6}{m+5}$．
（1）为实数；
（2）为虚数；
（3）为纯虚数．
14．如图可表示函数y=f（x）图象的是（　　）
A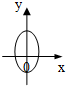．B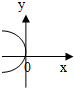．C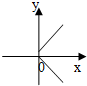．D．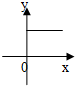
11．已知点An（n，an）（n∈N*）都在函数f（x）=logax（a＞0且a≠1）的图象上，则a2+a10与2a6的大小关系为（　　）
A．a2+a10＞2a6B．a2+a10＜2a6
C．a2+a10=2a6D．a2+a10与2a6的大小与a有关
18．在平行四边形ABCD中，AC与BD交于O，F是线段DC的三等分点，AF与CD交于点E，若$\overrightarrow{AB}=\overrightarrow a$，$\overrightarrow{AD}$=$\overrightarrow{b}$，则$\overrightarrow{AE}$等于（　　）
A．$\frac{1}{4}$$\overrightarrow{a}$+$\frac{3}{4}$$\overrightarrow{b}$B．$\frac{3}{4}\overrightarrow{a}$+$\frac{1}{4}\overrightarrow{b}$C．$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$D．$\frac{1}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$
8．“x＜-1”是“x2+x＞0”的（　　）条件．
A．充分而不必要B．必要而不充分
C．充分必要D．既不充分也不必要
15．已知$sin（α+\frac{π}{3}）=\frac{2}{3}$，其中$\frac{π}{6}＜α＜\frac{2π}{3}$，则cosα=$\frac{{2\sqrt{3}-\sqrt{5}}}{6}$．
12．给定椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0），称圆心在坐标原点O，半径为$\sqrt{{a^2}+{b^2}}$的圆是椭圆C的“伴随圆”，已知椭圆C的两个焦点分别是${F_1}（-\sqrt{2}，0），{F_2}（\sqrt{2}，0）$．
（1）若椭圆C上一动点M1满足|$\overrightarrow{{M_1}{F_1}}|+|\overrightarrow{{M_1}{F_2}}$|=4，求椭圆C及其“伴随圆”的方程；
（2）在（1）的条件下，过点P（0，t）（t＜0）作直线l与椭圆C只有一个交点，且截椭圆C的“伴随圆”所得弦长为2$\sqrt{3}$，求P点的坐标；
（3）已知m+n=-$\frac{cosθ}{sinθ}，mn=-\frac{3}{sinθ}（m≠n，θ∈（{0，π}））$，是否存在a，b，使椭圆C的“伴随圆”上的点到过两点（m，m2），（n，n2）的直线的最短距离dmin=$\sqrt{{a^2}+{b^2}}$-b．若存在，求出a，b的值；若不存在，请说明理由．
13．已知f（x）=ax，g（x）=logax，h（x）=xa，若0＜a＜1，则f（2），g（2），h（2）的大小关系是（　　）
A．f（2）＞g（2）＞h（2）B．g（2）＞f（2）＞h（2）C．h（2）＞g（2）＞f（2）D．h（2）＞f（2）＞g（2）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网