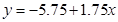题目内容
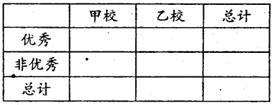
甲乙两个学校高三年级分别有1100人和1000人,为了了解这两个学校全体高三年级学生在该地区二模考试中的数学成绩情况,采用分层抽样方法从两个学校一共抽取了105名学生的数学成绩,并作出了如下的频数分布统汁表,规定考试成绩在[120,150]内为优秀.

(I)试求x,y的值;
(II)由以上统计数据填写右面2×2列联表,若按是否优秀来判断,是否有97.5%的把握
认为两个学校的数学成绩有差异。
(III)根据抽样结果分别估计甲校和乙校的优秀率,若把频率视为概率,现从乙校学生中任取3人,求优秀学生人数ξ的分布列和数学期望。
附:

(I)试求x,y的值;
(II)由以上统计数据填写右面2×2列联表,若按是否优秀来判断,是否有97.5%的把握
认为两个学校的数学成绩有差异。

(III)根据抽样结果分别估计甲校和乙校的优秀率,若把频率视为概率,现从乙校学生中任取3人,求优秀学生人数ξ的分布列和数学期望。
附:

(I)x=6,y=7(II)故有97.5%的把握认为,这两个学校的数学成绩有差异.
(III)E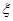 =3×
=3×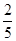 =
=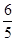
(III)E
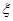 =3×
=3×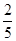 =
=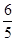
(I)先由分层抽样方法可知各层在样本中的占比与各层在总体中的占比相等。可求出x=6,y=7.
(II)由列联表知借助公式 可求出
可求出 的值确定这个结论的可信度。
的值确定这个结论的可信度。
(III)由题意知随机变量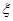 可能取的值有0,1,2,3.然后把每一个值对应的概率求出来,
可能取的值有0,1,2,3.然后把每一个值对应的概率求出来,
列出分布列,进而根据期望公式每一个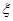 值与对应概率积之和求出数学期望
值与对应概率积之和求出数学期望
(I)由分层抽样知,甲校抽取了55人成绩,乙校抽取了50人的成绩.所以, x=6,y=7
(II)由以上统计数据填写右面2X2列联表如下:
因为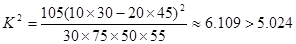 .
.
故有97.5%的把握认为,这两个学校的数学成绩有差异.…………8分
(III)由题意,可知:甲校的优秀率为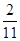 ,乙校的优秀率为
,乙校的优秀率为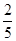 ,
,
由题意可知,随机变量§=0,1,2,3,且
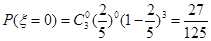
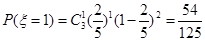


从而求得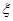 的分布列为:
的分布列为:
故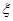 的数学期望E
的数学期望E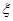 =3×
=3×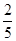 =
=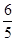
(II)由列联表知借助公式
 可求出
可求出 的值确定这个结论的可信度。
的值确定这个结论的可信度。(III)由题意知随机变量
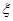 可能取的值有0,1,2,3.然后把每一个值对应的概率求出来,
可能取的值有0,1,2,3.然后把每一个值对应的概率求出来,列出分布列,进而根据期望公式每一个
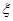 值与对应概率积之和求出数学期望
值与对应概率积之和求出数学期望(I)由分层抽样知,甲校抽取了55人成绩,乙校抽取了50人的成绩.所以, x=6,y=7
(II)由以上统计数据填写右面2X2列联表如下:
| | 甲校 | 乙校 | 总计 |
| 优秀 | 10 | 20 | 30 |
| 非优秀 | 45 | 30 | 75 |
| 总计 | 55 | 50 | 105 |
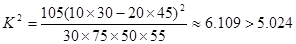 .
.故有97.5%的把握认为,这两个学校的数学成绩有差异.…………8分
(III)由题意,可知:甲校的优秀率为
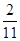 ,乙校的优秀率为
,乙校的优秀率为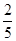 ,
,由题意可知,随机变量§=0,1,2,3,且

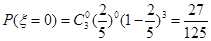
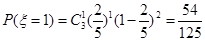


从而求得
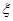 的分布列为:
的分布列为: 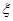 | 0 | 1 | 2 | 3 |
| P | 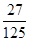 | 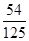 | 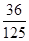 |  |
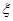 的数学期望E
的数学期望E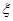 =3×
=3×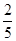 =
=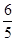

练习册系列答案
相关题目
 关于
关于 的线性回归方程
的线性回归方程 ;
; ,
, ,
,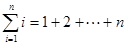
 (单位:度)与气温
(单位:度)与气温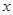 (单位:
(单位: )之间的关系,随机统计了某
)之间的关系,随机统计了某 天的用电量与当天气温,并制作了对照表:
天的用电量与当天气温,并制作了对照表:





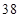

 ,当气温不低于
,当气温不低于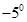 时,预测用电量最多为 度.
时,预测用电量最多为 度.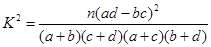
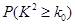
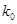

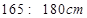 的概率;
的概率; 190cm之间的男生中任选2人,求至少有1人身高在185
190cm之间的男生中任选2人,求至少有1人身高在185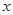 (单位:万元)与销售额
(单位:万元)与销售额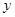 (单位:万元)之间的线性回归方程为
(单位:万元)之间的线性回归方程为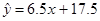 ,
,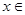 {2,4,5,6,8},则平均销售额
{2,4,5,6,8},则平均销售额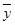 为( )
为( )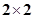 列联表得出
列联表得出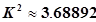 ,故有 把握认为婴儿的性别与出生时间有关系(利用下表解决问题)( )
,故有 把握认为婴儿的性别与出生时间有关系(利用下表解决问题)( )




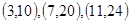 的回归方程是( ).
的回归方程是( ).