题目内容
【题目】如图动直线 
与抛物线 
交于点 
，与椭圆 
交于抛物线右侧的点 
为抛物线的焦点，则 
的最大值为（ ）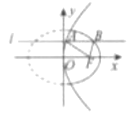
A.
B.
C.2
D.
【答案】D
【解析】抛物线的准线 
，焦点 
；椭圆 
的右焦点亦为 ；由抛物线定义可得 
，由椭圆的性质可知 
；∴ 
，由椭圆的性质可知， 
， 
时， 
取得最大值，最大值为 
，所以答案是：D．
【考点精析】认真审题，首先需要了解椭圆的概念(平面内与两个定点
，
的距离之和等于常数（大于
）的点的轨迹称为椭圆,这两个定点称为椭圆的焦点，两焦点的距离称为椭圆的焦距)，还要掌握抛物线的定义(平面内与一个定点
和一条定直线
的距离相等的点的轨迹称为抛物线．定点称为抛物线的焦点，定直线称为抛物线的准线)的相关知识才是答题的关键．
【题目】某市对大学生毕业后自主创业人员给予小额贷款补贴，贷款期限分为6个月、12个月、18个月、24个月、36个月五种，对于这五种期限的贷款政府分别补贴200元、300元、300元、400元、400元，从2016年享受此项政策的自主创业人员中抽取了100人进行调查统计，选取贷款期限的频数如表：
贷款期限 | 6个月 | 12个月 | 18个月 | 24个月 | 36个月 |
频数 | 20 | 40 | 20 | 10 | 10 |
以上表中各种贷款期限的频数作为2017年自主创业人员选择各种贷款期限的概率．
（Ⅰ）某大学2017年毕业生中共有3人准备申报此项贷款，计算其中恰有两人选择贷款期限为12个月的概率；
（Ⅱ）设给某享受此项政策的自主创业人员补贴为X元，写出X的分布列；该市政府要做预算，若预计2017年全市有600人申报此项贷款，则估计2017年该市共要补贴多少万元．
【题目】数独游戏越来越受人们喜爱，今年某地区科技馆组织数独比赛，该区甲、乙、丙、丁四所学校的学生积极参赛，参赛学生的人数如表所示：
中学 | 甲 | 乙 | 丙 | 丁 |
人数 | 30 | 40 | 20 | 10 |
为了解参赛学生的数独水平，该科技馆采用分层抽样的方法从这四所中学的参赛学生中抽取30名参加问卷调查．
（Ⅰ）问甲、乙、丙、丁四所中学各抽取多少名学生？
（Ⅱ）从参加问卷调查的30名学生中随机抽取2名，求这2名学生来自同一所中学的概率；
（Ⅲ）在参加问卷调查的30名学生中，从来自甲、丙两所中学的学生中随机抽取2名，用X表示抽得甲中学的学生人数，求X的分布列．