题目内容
【题目】已知数列![]() 满足
满足![]() .
.
(1)若![]() (
(![]() 且
且![]() ),数列
),数列![]() 为递增数列,求数列
为递增数列,求数列![]() 的通项公式;
的通项公式;
(2)若![]() (
(![]() 且
且![]() ),数列
),数列![]() 为递增数列,数列
为递增数列,数列![]() 为递减数列,且
为递减数列,且![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
【答案】(1)![]() ;(2)
;(2)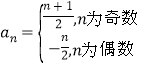 .
.
【解析】分析:(1)因为数列![]() 为递增数列,故可得
为递增数列,故可得![]() ,转化为
,转化为![]() ,结合
,结合![]() ,可得数列
,可得数列![]() 是首项
是首项![]() ,公差为1的等差数列,进而可得结果;(2)利用和(1)前半部分相同的思想可得
,公差为1的等差数列,进而可得结果;(2)利用和(1)前半部分相同的思想可得![]() 和
和![]() 成立,紧接着分为
成立,紧接着分为![]() 为奇数或者
为奇数或者![]() 为偶数即可.
为偶数即可.
详解:(1)因为数列![]() 为递增数列,所以
为递增数列,所以![]() ,即
,即![]() ,
,
![]() ,由条件,
,由条件,![]() ,
,
所以![]() ,
,
即数列![]() 是首项
是首项![]() ,公差为1的等差数列,
,公差为1的等差数列,
则![]() .
.
(2)因为数列![]() 为递增数列,
为递增数列,
所以![]() ,即
,即![]() ,
,
![]() ,由条件
,由条件![]() ,
,
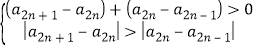 ,
,
得![]() (绝对值大的必为正数),
(绝对值大的必为正数),![]() ,
,
同理,数列![]() 为递减数列,所以
为递减数列,所以![]() ,即
,即![]() ,
,
![]() ,由条件,
,由条件,
![]() ,
,
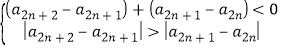 ,
,
得![]() (绝对值大的必为负数),
(绝对值大的必为负数),![]() ,
,
而![]() ,则
,则![]() ,
,
综上可知,当![]() 为奇数且
为奇数且![]() 时,
时,![]() ;
;
当![]() 为偶数时,
为偶数时,![]() .
.
当![]() 为奇数且
为奇数且![]() 时,
时,
![]()
![]()
![]() ,
,
当![]() 时,
时,![]() 也成立,
也成立,
即当![]() 为奇数时,
为奇数时,![]() ,
,
当![]() 为偶数时,
为偶数时,![]() 为奇数,
为奇数,![]() ,
,
所以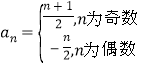 .
.

练习册系列答案
相关题目