题目内容
(2012•黄州区模拟)已知集合A={x∈R|
≤2},集合B={a∈R|已知函数f(x)=
-1+lnx,?x0>0,使f(x0)≤0成立},则A∩B=( )
| x+1 |
| 2x-1 |
| a |
| x |
分析:解分式不等式求出集合A,根据集合B可得a≤x-xlnx 在(0,+∞)上有解.利用导数求得h(x)=x-xlnx的值域为(-∞,1],要使不等式a≤xlnx 在(0,+∞)上有解,
只要a小于或等于h(x)的最大值即可,即a≤1 成立,故B={a|a≤1},由此求得A∩B.
只要a小于或等于h(x)的最大值即可,即a≤1 成立,故B={a|a≤1},由此求得A∩B.
解答:解:集合A={x∈R|
≤2}={x|
≤0}={x|
≥0 }={x|(x-1)(2x-1)≥0,且2x-1≠0}
={x|x<
,或 x≥1}.
由集合B 可知f(x)的定义域为{x|x>0},不等式
-1+lnx≤0有解,
即不等式a≤x-xlnx 在(0,+∞)上有解.
令h(x)=x-xlnx,可得h′(x)=1-(lnx+1)=-lnx,令h′(x)=0,可得 x=1.
再由当0<x<1 时,h′(x)>0,当x>1 时,h′(x)<0,可得当x=1时,h(x)=x-xlnx 取得最大值为 1.
要使不等式a≤x-xlnx 在(0,+∞)上有解,只要a小于或等于h(x)的最大值即可.
即a≤1 成立,所以集合B={a|a≤1}.
所以A∩B={x|x<
,或 x=1}.
故选C.
| x+1 |
| 2x-1 |
| 3-3x |
| 2x-1 |
| x-1 |
| 2x-1 |
={x|x<
| 1 |
| 2 |
由集合B 可知f(x)的定义域为{x|x>0},不等式
| a |
| x |
即不等式a≤x-xlnx 在(0,+∞)上有解.
令h(x)=x-xlnx,可得h′(x)=1-(lnx+1)=-lnx,令h′(x)=0,可得 x=1.
再由当0<x<1 时,h′(x)>0,当x>1 时,h′(x)<0,可得当x=1时,h(x)=x-xlnx 取得最大值为 1.
要使不等式a≤x-xlnx 在(0,+∞)上有解,只要a小于或等于h(x)的最大值即可.
即a≤1 成立,所以集合B={a|a≤1}.
所以A∩B={x|x<
| 1 |
| 2 |
故选C.
点评:本题主要考查集合的表示方法、分式不等式的解法,利用导数判断函数的单调性,根据函数的单调性求函数的值域,两个集合的交集的定义和求法,属于中档题.

练习册系列答案
相关题目
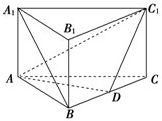 (2012•黄州区模拟)如图,在直三棱柱ABC-A1B1C1中,AB=BC=2AA1,∠ABC=90°,D是BC的中点.
(2012•黄州区模拟)如图,在直三棱柱ABC-A1B1C1中,AB=BC=2AA1,∠ABC=90°,D是BC的中点. (2012•黄州区模拟)已知某几何体的三视图如图,则该几何体的表面积为
(2012•黄州区模拟)已知某几何体的三视图如图,则该几何体的表面积为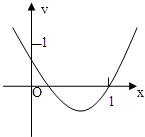 (2012•黄州区模拟)如图是二次函数f(x)=x2-bx+a的部分图象,则函数g(x)=2lnx+f(x)在点(b,g(b))处切线的斜率的最小值是( )
(2012•黄州区模拟)如图是二次函数f(x)=x2-bx+a的部分图象,则函数g(x)=2lnx+f(x)在点(b,g(b))处切线的斜率的最小值是( )