题目内容
【题目】已知向量 
=（1， 
）， 
=（sinx，cosx），设函数f（x）=
（1）求函数f（x）的最小正周期和最大值；
（2）设锐角△ABC的三个内角A，B，C的对边分别为a，b，c，若c= 
，cosB= 
，且f（C）= ，求b．
【答案】
（1）解：f（x）=sinx+ 
cosx=2sin（x+ 
），
∴f（x）的最小正周期T=2π，f（x）的最大值为2
（2）解：∵f（C）=2sin（C+ ）= ，∴sin（C+ ）= 
，
∵0 
，∴C= ．
∵cosB= 
，∴sinB= 
．
由正弦定理得 
，∴ 
，
解得：b= 
．
【解析】（1）根据向量的数量积公式得出f（x）解析式，使用和角公式化简，结合正弦函数的性质得出答案；（2）根据f（C）= 得出C，根据同角三角函数的关系计算sinB，由正弦定理得出b．
【考点精析】解答此题的关键在于理解正弦定理的定义的相关知识，掌握正弦定理:
，以及对余弦定理的定义的理解，了解余弦定理:
;
;
．
练习册系列答案
名校联盟快乐课堂系列答案
黄冈创优卷系列答案
相关题目
【题目】某书店销售刚刚上市的某知名品牌的高三数学单元卷，按事先拟定的价格进行5天试销，每种单价试销1天，得到如下数据：
单价 | 18 | 19 | 20 | 21 | 22 |
销量 | 61 | 56 | 50 | 48 | 45 |
（1）求试销5天的销量的方差和
对
的回归直线方程；
（2）预计今后的销售中，销量与单价服从（1）中的回归方程，已知每册单元卷的成本是14元，为了获得最大利润，该单元卷的单价卷的单价应定为多少元？
（附：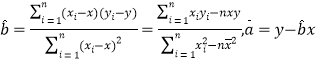
）
