题目内容
已知数列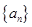 满足条件
满足条件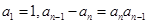 , 则
, 则 .
.
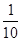
解析试题分析:由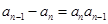 得
得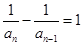 且
且 ,所以数列
,所以数列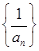 是以1为首项,1为公差的等差数列,所以
是以1为首项,1为公差的等差数列,所以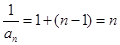 ,进而可得
,进而可得 ,所以
,所以 .
.
考点:1.由递推关系求数列的通项;2.等差数列的通项公式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
已知数列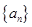 满足条件
满足条件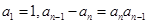 , 则
, 则 .
.
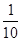
解析试题分析:由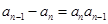 得
得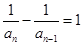 且
且 ,所以数列
,所以数列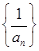 是以1为首项,1为公差的等差数列,所以
是以1为首项,1为公差的等差数列,所以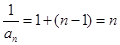 ,进而可得
,进而可得 ,所以
,所以 .
.
考点:1.由递推关系求数列的通项;2.等差数列的通项公式.

 名校课堂系列答案
名校课堂系列答案