Question

【题目】已知函数f（x）=xcos+a，a∈R.

（I）求曲线y=f（x）在点x=处的切线的斜率；

（II）判断方程f '（x）=0（f '（x）为f（x）的导数）在区间（0，1）内的根的个数，说明理由；

（III）若函数F（x）=xsinx+cosx+ax在区间（0，1）内有且只有一个极值点，求a的取值范围.

Answer 1

【答案】（I）. （II）1个；（III）-cos1a<0.

【解析】试题分析：（1）取出函数的导函数，可得在点处的导数值，即可得到切线的斜率；

（2）设，求其导数，可得当时， ，则函数为减函数，结合，可得有且只有一个，使成立，即方程在区间内有且仅有一个实数解；

（3）把函数在区间内有且只有一个极值点，转化为在区间内有且只有一个零点，且在两侧异号，然后结合（2）中的单调性，列出不等式组，即可求解实数的取值范围.

试题解析：

（I）f '（x）=cosx-xsinx·k=f '（）=.

（II）设g（x）=f '（x），g' （x）=-sinx-（sin x+xcosx）=-2sinx-xcosx.

当x∈（0，1）时，g '（x）<0，则函数g（x）为减函数.

又因为g（0）=1>0，g（1）=cos1-sin1<0，

所以有且只有一个x0∈（0，1），使g（x0）=0成立.

所以函数g（x）在区间（0，1）内有且只有一个零点，即方程f '（x）=0在区间（0，1）内有且只有一个实数根.

（III）若函数F（x）=xsinx+cosx+ax在区间（0，1）内有且只有一个极值点，由于F '（x）=f（x），即f（x）=xcosx+a在区间（0，1）内有且只有一个零点x1，且f（x）在x1两侧异号.

因为当x∈（0，1）时，函数g（x）为减函数，所以在（0，x0）上，g（x）>g（x0）=0，即f '（x）>0成立，函数f（x）为增函数；

在（x0，1）上，g（x）<g（x0）=0，即f '（x）<0成立，函数f（x）为减函数.

则函数f（x）在x=x0处取得极大值f（x0）.

当f（x0）=0时，虽然函数f（x）在区间（0，1）内有且只有一个零点x0，但f（x）在x0两侧同号，不满足F（x）在区间（0，1）内有且只有一个极值点的要求.

由于f（1）=a+cos1，f（0）=a，显然f（1）>f（0）.

若函数f（x）在区间（0，1）内有且只有一个零点x1，且f（x）在x1两侧异号，

则只需满足：

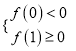.即，解得-cos1a<0.