题目内容
16. 如图,已知圆C的圆心在直线l:y=2x-4上,半径为1,点A(0,3).
如图,已知圆C的圆心在直线l:y=2x-4上,半径为1,点A(0,3).(Ⅰ)若圆心C也在直线y=x-1上,过点A作圆C的切线,求切线的方程;
(Ⅱ)若圆C上存在点M,使|MA|=2|MO|(O为坐标原点),求圆心C的横坐标a的取值范围.
分析 (Ⅰ)求出圆心C的坐标,设出点A作圆C的切线方程,利用点到直线的距离等于半径,然后求切线的方程;
(Ⅱ)设出圆C的方程,点M的坐标,利用|MA|=2|MO|,求出M的轨迹,通过两个圆的位置关系,求圆心C的横坐标a的取值范围.
解答 解:(Ⅰ)由$\left\{\begin{array}{l}y=2x-4\\ y=x-1\end{array}\right.$,得圆心C(3,2),过点A作圆C的切线斜率存在,设A点的圆C的切线的方程:y=kx+3,即kx-y+3=0.由题意,$\frac{|3k+1|}{\sqrt{{k}^{2}+1}}=1$,解得k=0,k=$-\frac{3}{4}$,所求切线方程为:y=3或3x+4y-12=0;
(Ⅱ)∵圆C的圆心在直线l:y=2x-4上,
∴圆C的方程设为:(x-a)2+(y-(2a-4))2=1,设M(x,y),由|MA|=2|MO|,可得:$\sqrt{{x}^{2}+(y-3)^{2}}=2\sqrt{{x}^{2}+{y}^{2}}$,化简可得x2+(y+1)2=4,点M在以D(0,-1)为圆心,2为半径的圆上.
由题意,点M(x,y)在圆上,
∴圆C和圆D有公共点,则|2-1|≤|CD|≤2+1,
∴1$≤\sqrt{{(a-0)}^{2}+[(2a-4)-(-1)]^{2}}$≤3,即1$≤\sqrt{{5a}^{2}{-12a+9}^{\;}}≤3$,5a2-12a+8≥0,可得a∈R,由5a2-12a≤0,可得0$≤a≤\frac{12}{5}$,
圆心C的横坐标a的取值范围:$[0,\frac{12}{5}]$.
点评 本题考查直线与圆的位置关系的综合应用,考查转化思想以及计算能力.

练习册系列答案
相关题目
8.已知Rt△ABC中,AB=AC=a,AD是斜边上的高,以AD为折痕使∠BDC成直角.则折后几何体中,∠BAC的度数为( )
| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
6.已知M是△ABC内一点,且$\overrightarrow{AB}•\overrightarrow{AC}=2\sqrt{3},∠BAC={30°}$,若△MBC,△MCA,△MAB的面积分别为$\frac{1}{2},x,y$,则xy的最大值是( )
| A. | $\frac{1}{14}$ | B. | $\frac{1}{16}$ | C. | $\frac{1}{18}$ | D. | $\frac{1}{20}$ |
 如图,在直棱柱ABCD-A1B1C1D1中,AD∥BC,∠BAC=90°,AB=$\sqrt{3}$,BC=1,AD=AA1=3.
如图,在直棱柱ABCD-A1B1C1D1中,AD∥BC,∠BAC=90°,AB=$\sqrt{3}$,BC=1,AD=AA1=3. 如图,在棱长为1的正方体ABCD-A1B1C1D1中,M、N分别是BB1,BC的中点,(1)直线MN与平面BDD1B1所成角的余弦值为$\frac{\sqrt{3}}{2}$
如图,在棱长为1的正方体ABCD-A1B1C1D1中,M、N分别是BB1,BC的中点,(1)直线MN与平面BDD1B1所成角的余弦值为$\frac{\sqrt{3}}{2}$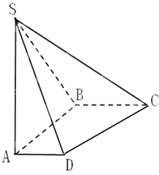 如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,AD∥BC,SA⊥平面ABCD,SA=AB=BC=1,AD=$\frac{1}{2}$
如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,AD∥BC,SA⊥平面ABCD,SA=AB=BC=1,AD=$\frac{1}{2}$ 如图,已知AE⊥平面CDE,四边形ABCD为正方形,M,N分别是线段BE,DE的中点.
如图,已知AE⊥平面CDE,四边形ABCD为正方形,M,N分别是线段BE,DE的中点.