题目内容
【题目】已知函数f（x）是定义在R上的偶函数，且在[0，+∞）上单调递减，f（2）＝0，则不等式f（log2x）＞0的解集为（ ）
A.（
，4）B.（2，2）C.（，+∞）D.（4，+∞）
【答案】A
【解析】
根据题意，由函数f（x）的奇偶性与f（2）＝0可得f（log2x）＞0f（|log2x|）＞f（2），结合函数f（x）的单调性分析可原不等式等价于|log2x|＜2，解可得x的取值范围，即可得答案.
根据题意，函数f（x）是定义在R上的偶函数，且f（2）＝0，
则f（log2x）＞0f（|log2x|）＞f（2），
又由f（x）在[0，+∞）上单调递减，f（|log2x|）＞f（2）|log2x|＜2，
变形可得：﹣2＜log2x＜2，
解得：
x＜2，不等式的解集为（
，2）；
故选：A.
名师点睛字词句段篇系列答案
【题目】某中学高三(3)班有学生50人，现调查该班学生每周平均体育锻炼时间的情况，得到如下频率分布直方图，其中数据的分组区间为：
，
，
，
，
，
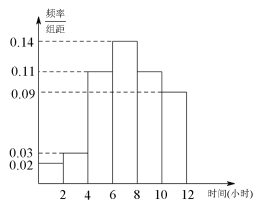
(1)从每周平均体育锻炼时间在
的学生中，随机抽取2人进行调查，求这2人的每周平均体育锻炼时间都超过2小时的概率；
(2)已知全班学生中有40%是女姓，其中恰有3个女生的每周平均体育锻炼时间不超过4小时，若每周平均体育锻炼时间超过4小时称为经常锻炼，问：有没有90%的把握说明，经常锻炼与否与性别有关？
附：
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
【题目】某地计划在水库建一座至多安装3台发电机的水电站.过去50年的水文资料显示，水库年入流量
（年入流量：一年内上游来水与库区降水之和.单位：亿立方米）都在40以上，其中，不足80的年份有10年，不低于80且不超过120的年份有35年，超过120的年份有5年，将年入流量在以上三段的频率作为相应段的概率，并假设各年的年入流量相互独立.
（1）求未来4年中，至多有1年的年入流量超过120的概率；
（2）水电站希望安装的发电机尽可能运行，但每年发电机最多可运行台数受年入流量限制，并有如下关系：
年入流量 |
|
|
|
发电机最多可运行台数 | 1 | 2 | 3 |
若某台发电机运行，则该台发电机年净利润为5000万元；若某台发电机未运行，则该台发电机年维护费与年入流量有如下关系：
年入流量 |
|
|
一台未运行发电机年维护费 | 500 | 800 |
欲使水电站年净利润最大，应安装发电机多少台？
