题目内容
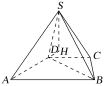
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是梯形,
是梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,侧面
,侧面![]() 底面
底面![]() .
.
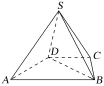
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,且三棱锥
,且三棱锥![]() 的体积为
的体积为![]() ,求侧面
,求侧面![]() 的面积.
的面积.
【答案】(1)证明见解析; (2)![]() .
.
【解析】
(1)由梯形![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,运用勾股定理和余弦定理,可得
,运用勾股定理和余弦定理,可得![]() ,由线面垂直的判定定理可得
,由线面垂直的判定定理可得![]() 平面
平面![]() ,运用面面垂直的判定定理即可得证;
,运用面面垂直的判定定理即可得证;
(2)运用面面垂直的性质定理,以及三棱锥的体积公式,求得![]() ,运用勾股定理和余弦定理,可得
,运用勾股定理和余弦定理,可得![]() ,
,![]() ,运用三角形的面积公式,即可得到所求值.
,运用三角形的面积公式,即可得到所求值.
(1)在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,在直角三角形
,在直角三角形![]() 中,
中,![]() ,
,
可得![]() ,
,![]() ,
,![]() ,
,
由余弦定理可得![]() ,
,
则![]() ,由面
,由面![]() 底面
底面![]() ,
,
所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() ;
;
(2)解:![]() ,且三棱锥
,且三棱锥![]() 的体积为
的体积为![]() ,
,
由![]() ,
,
在![]() 中,可得
中,可得![]() ,
,
![]() 的边
的边![]() 上的高
上的高![]() ,
,
由![]() 平面
平面![]() ,可得
,可得
![]() ,
,
解得![]() ,
,
由![]() 平面
平面![]() ,可得
,可得![]() ,
,
![]() ,
,
又![]() ,
,
在等腰三角形![]() 中,
中,
边![]() 上的高为
上的高为![]() ,
,
则![]() 的面积为
的面积为![]() .
.

【题目】某市教育局为了监控某校高一年级的素质教育过程,从该校高一年级16个班随机抽取了16个样本成绩,制表如下:
抽取次序 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
测评成绩 | 95 | 96 | 96 | 90 | 95 | 98 | 98 | 97 |
抽取次序 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
测评成绩 | 97 | 95 | 96 | 98 | 99 | 96 | 99 | 96 |
令![]() 为抽取的第
为抽取的第![]() 个学生的素质教育测评成绩,
个学生的素质教育测评成绩,![]() ,经计算得,
,经计算得,![]() ,
,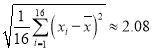 .以下计算精确到0.01.
.以下计算精确到0.01.
(1)设![]() 为抽取的16个样本的成绩,用频率估计概率,求
为抽取的16个样本的成绩,用频率估计概率,求![]() 的分布列、数学期望
的分布列、数学期望![]() 和标准方差
和标准方差![]() ;
;
(2)在抽取的样本成绩中,如果出现了在![]() 之外的成绩,就认为本学期的素质教育过程可能出现了异常情况,需对本学期的素质教学过程进行反思,同时对下学期的素质教育过程提出指导性的建议.从该校抽样的结果来看,是否需对本学期的素质教学过程进行反思,同时对下学期的素质教育过程提出指导性的建议?
之外的成绩,就认为本学期的素质教育过程可能出现了异常情况,需对本学期的素质教学过程进行反思,同时对下学期的素质教育过程提出指导性的建议.从该校抽样的结果来看,是否需对本学期的素质教学过程进行反思,同时对下学期的素质教育过程提出指导性的建议?
(3)列出不小于![]() 的所有样本成绩,设列出的这些成绩的中位数为
的所有样本成绩,设列出的这些成绩的中位数为![]() ,每次从列出的这些成绩中随机抽取1个成绩,有放回地连续抽取3次,求恰好有2次抽得的成绩为
,每次从列出的这些成绩中随机抽取1个成绩,有放回地连续抽取3次,求恰好有2次抽得的成绩为![]() 的概率.
的概率.