题目内容
在△ABC中,已知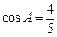 ,
,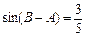 ,求
,求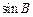 的值.
的值.
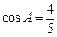 ,
,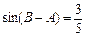 ,求
,求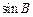 的值.
的值.sinB=

在△ABC中,cosA=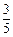 ,∴sinA=
,∴sinA=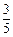 .又sin(B-A)=
.又sin(B-A)=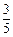 ,∴ 0<B-A<π.
,∴ 0<B-A<π.
∴cos(B-A)=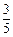 ,或cos(B-A)=
,或cos(B-A)=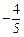 .……6分若cos(B-A)=
.……6分若cos(B-A)=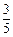 ,则sinB=sin[A+(B-A)]
,则sinB=sin[A+(B-A)]
=sinAcos(B-A)+cosAsin(B-A)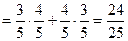 .…12分若cos(B-A)=
.…12分若cos(B-A)=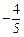 ,
,
则sinB=sin[A+(B-A)]=sinAcos(B-A)+cosAsin(B-A) (舍去).
(舍去).
综上所述,得sinB=
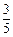 ,∴sinA=
,∴sinA=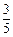 .又sin(B-A)=
.又sin(B-A)=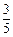 ,∴ 0<B-A<π.
,∴ 0<B-A<π.∴cos(B-A)=
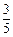 ,或cos(B-A)=
,或cos(B-A)=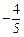 .……6分若cos(B-A)=
.……6分若cos(B-A)=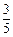 ,则sinB=sin[A+(B-A)]
,则sinB=sin[A+(B-A)]=sinAcos(B-A)+cosAsin(B-A)
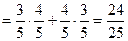 .…12分若cos(B-A)=
.…12分若cos(B-A)=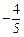 ,
,则sinB=sin[A+(B-A)]=sinAcos(B-A)+cosAsin(B-A)
 (舍去).
(舍去).综上所述,得sinB=


练习册系列答案
相关题目
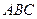 中,角
中,角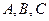 所对的边分别为
所对的边分别为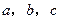 ,
,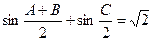 .
.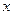 的方程
的方程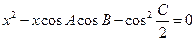 有一根为
有一根为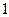 ,则
,则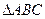 是
是 三角形.
三角形.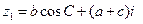 ,
,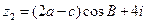 ,且
,且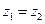 ,其中
,其中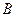 、
、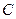 为△ABC的内角,
为△ABC的内角,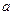 、
、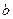 、
、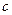 为角
为角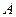 、
、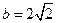 ,求△ABC的面积.
,求△ABC的面积.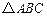
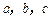
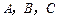
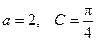
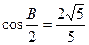
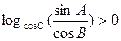 (B)
(B)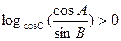
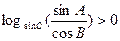 (D)
(D)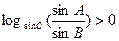
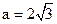 ,b=2,△ABC的面积S=
,b=2,△ABC的面积S=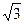 ,求第三边c.
,求第三边c.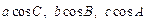 成等差数列.(Ⅰ)求B的值;(Ⅱ)求
成等差数列.(Ⅰ)求B的值;(Ⅱ)求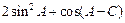 的范围.
的范围.