题目内容
(本小题15分)在各项为正的数列 中,数列的前n项和
中,数列的前n项和 满足
满足
(1) 求 ;(2) 由(1)猜想数列
;(2) 由(1)猜想数列 的通项公式并证明,(3) 求
的通项公式并证明,(3) 求
 中,数列的前n项和
中,数列的前n项和 满足
满足
(1) 求
 ;(2) 由(1)猜想数列
;(2) 由(1)猜想数列 的通项公式并证明,(3) 求
的通项公式并证明,(3) 求
解:
(1)a1=1,a2= ,a3=
,a3= ;
;
(2)数列{an}的通项公式可能是:an= ,证明见解析。
,证明见解析。
(3)Sn= =
=
(1)a1=1,a2=
 ,a3=
,a3= ;
;(2)数列{an}的通项公式可能是:an=
 ,证明见解析。
,证明见解析。(3)Sn=
 =
=
本试题主要是考查了数列的通项公式与前n项和的关系式的运用,令值的思想得到前几项,然后归纳猜想数列的通项公式,并运用数学归纳法证明,
(1)由题意可知 ,那么对于n令值,那么可知a2=
,那么对于n令值,那么可知a2=
a3=
(2)根据上一问的结论,数列{an}的通项公式可能是:an= ,然后运用数学归纳法分两步骤证明即可。
,然后运用数学归纳法分两步骤证明即可。
(3)因为通项公式累加可以得到前n项和的结论。
解:
(1)S1=1/2(a1+1/a1)
又S1=a1
故1/2(a1+1/a1)=a1
即a12=1 因为a1>0
故a1=1
S2=1/2(a2+1/a2)
又S2=a1+a2=1+a2
故1/2(a2+1/a2)=1+a2 (a2>0)
解得:a2=
同理:a3=
(2)从(1)中可看出:数列{an}的通项公式可能是:an=
假设an= 成立
成立
证明:
① 当n=1时,an=1= 假设成立
假设成立
② 当n=2时,an= =
= 假设成立
假设成立
③ 假设n=i时,假设成立,即
ai=
Si=( +(
+( )+(
)+( )+…+(
)+…+( )=
)=
那么,当n=i+1时
由sn=1/2(an+1/an)得
Si+1=1/2(ai+1+1/ai+1)
ai+1="Si+1-Si=1/2(ai+1+1/ai+1)-"
解得:ai+1= 由①②③可证明假设an=
由①②③可证明假设an= 成立
成立
an通项公式为:an=
(3)Sn= =
=
(1)由题意可知
 ,那么对于n令值,那么可知a2=
,那么对于n令值,那么可知a2=
a3=

(2)根据上一问的结论,数列{an}的通项公式可能是:an=
 ,然后运用数学归纳法分两步骤证明即可。
,然后运用数学归纳法分两步骤证明即可。(3)因为通项公式累加可以得到前n项和的结论。
解:
(1)S1=1/2(a1+1/a1)
又S1=a1
故1/2(a1+1/a1)=a1
即a12=1 因为a1>0
故a1=1
S2=1/2(a2+1/a2)
又S2=a1+a2=1+a2
故1/2(a2+1/a2)=1+a2 (a2>0)
解得:a2=

同理:a3=

(2)从(1)中可看出:数列{an}的通项公式可能是:an=

假设an=
 成立
成立证明:
① 当n=1时,an=1=
 假设成立
假设成立② 当n=2时,an=
 =
= 假设成立
假设成立③ 假设n=i时,假设成立,即
ai=

Si=(
 +(
+( )+(
)+( )+…+(
)+…+( )=
)=
那么,当n=i+1时
由sn=1/2(an+1/an)得
Si+1=1/2(ai+1+1/ai+1)
ai+1="Si+1-Si=1/2(ai+1+1/ai+1)-"

解得:ai+1=
 由①②③可证明假设an=
由①②③可证明假设an= 成立
成立an通项公式为:an=

(3)Sn=
 =
=

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
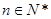 时,令
时,令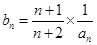 ,
,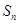 是数列{bn}的前n项和,求证:
是数列{bn}的前n项和,求证: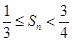
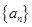 的前
的前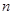 和为
和为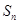 ,其中
,其中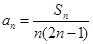 且
且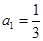
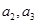
 的前
的前 项和为
项和为 .若
.若 ,
, ,则
,则 ( )
( )



 满足:
满足: ,
, ,求数列
,求数列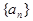 是等和数列,且
是等和数列,且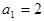 ,公和为5,那么
,公和为5,那么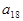 的值为: _ ;这个数列的前n项和
的值为: _ ;这个数列的前n项和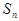 的计算公式为:_ ___.
的计算公式为:_ ___.  当
当 时,观察下列等式:
时,观察下列等式: ,
,  ,
, ,
,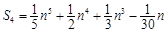 ,
, ,
, .
. 
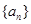 的前
的前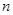 项和为
项和为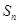 ,若点
,若点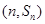 (
(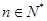 )在函数
)在函数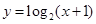 的反函数的图像上,则
的反函数的图像上,则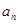 =________.
=________. 的前
的前 项和
项和 ,则
,则 的值是( )
的值是( )


